题目内容
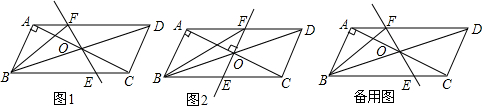
17.如图,在平行四边形ABCD中,AB⊥AC,对角线AC,BD相交于点O,将直线AC绕点O顺时针旋转一个角度α(0°<α≤90°),分别交线段BC,AD于点E,F,连接BF.(1)如图1,在旋转的过程中,写出线段AF于EC的数量关系,并证明;
(2)如图2,当旋转至90°时,判断四边形ABEF的形状,并证明;
(3)若AB=1,BC=$\sqrt{5}$,当α=45°时,线段BF与DF相等.
分析 (1)根据平行四边形的性质得AD∥CB,OA=OC,则∠FAO=∠ECO,于是可判断△AOF≌△COE,则AF=CE;
(2)由于∠AOF=90°,∠BAC=90°,可判断AB∥EF,易得四边形ABEF为平行四边形;
(3)先根据勾股定理计算出AC=2,由平行四边形的性质得OA=1,则可判断△ABO为等腰直角三角形,所以∠AOB=45°,由于当∠FBD=∠FDB时,BF=DF,加上∠FDB=∠CBD,所以∠FBD=∠CBD,即BO平分∠EBF,根据等腰三角形的性质得OB⊥EF,于是可计算出∠AOF=45°,再利用旋转的性质即可得到α的度数.
解答 解:(1)AF=CE.理由如下:
∵四边形ABCD为平行四边形,
∴AD∥CB,OA=OC,
∴∠FAO=∠ECO,
在△AOF和△COE中
$\left\{\begin{array}{l}{∠FAO=∠ECO}\\{AO=CO}\\{∠AOF=∠COE}\end{array}\right.$,
∴△AOF≌△COE,
∴AF=CE;
(2)当旋转至90°时,四边形ABEF为平行四边形.理由如下:
∵∠AOF=90°,∠BAC=90°,
∴AB∥EF,
而AF∥BE,
∴四边形ABEF为平行四边形;
(3)在Rt△ABC中,∵AB=1,BC=$\sqrt{5}$,
∴AC=$\sqrt{(\sqrt{5})^{2}-{1}^{2}}$=2,
∴OA=1,
∴△ABO为等腰直角三角形,
∴∠AOB=45°,
当∠FBD=∠FDB时,BF=DF,
而∠FDB=∠CBD,
∴∠FBD=∠CBD,
即BO平分∠EBF,
∵OE=OF,
∴OB⊥EF,
∴∠BOF=90°,
∴∠AOF=90°-45°=45°,
即α=45°.
故答案为45.
点评 本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了平行四边形的判定与性质.

 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案| A. | -3,-2,-1 | B. | -2,-1 | C. | -4,-3,-2,-1 | D. | -3,-2,-1,0 |
 已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=-$\frac{1}{3}$,其图象如图所示,则下面信息正确的是( )
已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=-$\frac{1}{3}$,其图象如图所示,则下面信息正确的是( )| A. | abc<0 | B. | a+b+c>0 | C. | a-2b+4c<0 | D. | b+2c>0 |
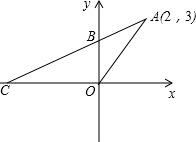 如图所示,已知一次函数y=kx+b的图象经过点A(2,3)和点B(0,2),且与x轴相交于点C.
如图所示,已知一次函数y=kx+b的图象经过点A(2,3)和点B(0,2),且与x轴相交于点C.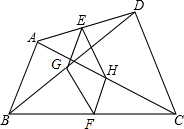 如图,任意四边形ABCD中,点E、F、G、H分别是AD、BC、BD、AC的中点,给四边形ABCD添加一个条件,使四边形EGFH是菱形,你添加的一个条件是AB=CD.请加以说明.
如图,任意四边形ABCD中,点E、F、G、H分别是AD、BC、BD、AC的中点,给四边形ABCD添加一个条件,使四边形EGFH是菱形,你添加的一个条件是AB=CD.请加以说明.