题目内容
1．已知：1+3=4=22，1+3+5=9=32，1+3+5+7=16=42，1+3+5+7+9=25=52，…，根据前面各式的规律可猜测：101+103+105+…+199=7500．分析 根据题意知，从1开始的连续奇数的和等于首尾两个奇数的和的一半的平方，用从1开始到199的奇数的和减去从1开始到99的奇数的和，列式计算即可得解．
解答 解：101+103+10 5+107+…+195+197+199=（$\frac{1+199}{2}$）2-（$\frac{1+99}{2}$）2；
=1002-502，
=10000-2500，
=7500，
故答案为：7500．
点评 此题主要考查了数字变化规律，得出从奇数1开始，连续奇数的和等于数的个数的平方是解题关键．
练习册系列答案
习题精选系列答案
相关题目
12．如图是几个相同的小正方体搭成的几何体的三视图，则搭成这个几何体的小正方体有（ ）
| A． | 4个 | B． | 5个 | C． | 6个 | D． | 7个 |
9．
某车站在春运期间为改进服务，随机抽样调查了100名旅客从开始在购票窗口排队到购到车票所用的时间t（以下简称购票用时，单位为分钟）．下面是这次调查统计分析得到的频率分布表和频率分布直方图．解答下列问题：
（1）这次抽样的样本容量是多少？
（2）在表中填写出缺失的数据并补全频率分布直方图：
（3）旅客购票用时的平均数可能落在哪一小组？
（4）若每增加一个购票窗口可以使平均购票用时降低5分钟，要使平均购票用时不超过10分钟，那么请你估计最少需增加几个窗口？
某车站在春运期间为改进服务，随机抽样调查了100名旅客从开始在购票窗口排队到购到车票所用的时间t（以下简称购票用时，单位为分钟）．下面是这次调查统计分析得到的频率分布表和频率分布直方图．解答下列问题：| 分 组 | 频数 | 频率 | |
| 一组 | 0≤t＜5 | 0 | 0 |
| 二组 | 5≤t＜10 | 10 | 0.10 |
| 三组 | 10≤t＜15 | 10 | 0.10 |
| 四组 | 15≤t＜20 | 50 | 0.50 |
| 五组 | 20≤t＜25 | 30 | 0.30 |
| 合 计 | 100 | 1 | |
（2）在表中填写出缺失的数据并补全频率分布直方图：
（3）旅客购票用时的平均数可能落在哪一小组？
（4）若每增加一个购票窗口可以使平均购票用时降低5分钟，要使平均购票用时不超过10分钟，那么请你估计最少需增加几个窗口？
16．
正方形ABCD的边长为1，其面积记为S1，以CD为斜边作等腰直角三角形，以该等腰直角三角形的一条直角边为边向外作正方形，其面积记为S2，…按此规律继续下去，则S9的值为（ ）
正方形ABCD的边长为1，其面积记为S1，以CD为斜边作等腰直角三角形，以该等腰直角三角形的一条直角边为边向外作正方形，其面积记为S2，…按此规律继续下去，则S9的值为（ ）| A． | ${（{\frac{1}{2}}）^9}$ | B． | ${（{\frac{1}{2}}）^8}$ | C． | ${（{\frac{{\sqrt{2}}}{2}}）^9}$ | D． | ${（{\frac{{\sqrt{2}}}{2}}）^8}$ |
6．
已知一次函数y=mx+n-3的图象如图，则m、n的取值范围是（ ）
已知一次函数y=mx+n-3的图象如图，则m、n的取值范围是（ ）| A． | m＞0，n＜3 | B． | m＜0，n＞3 | C． | m＜0，n＜3 | D． | m＞0，n＞3 |
有一直经为$\sqrt{2}$cm圆形纸片，从中剪出一个圆心角是90°的最大扇形ABC（如图所示）．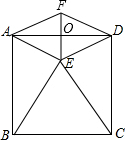
如图，正方形ABCD的边长为2，以BC为边向正方形内作等边△BCE，连接AE、DE．