题目内容
9. 如图,在Rt△ABC中,∠ACB=90°,∠ABC的平分线BD交AC于点D,DE⊥DB交AB于点E,△BDE的外接圆⊙O交BC于点F.
如图,在Rt△ABC中,∠ACB=90°,∠ABC的平分线BD交AC于点D,DE⊥DB交AB于点E,△BDE的外接圆⊙O交BC于点F.(1)求证:AC是⊙O的切线;
(2)若⊙O的半径为5cm,BC=8cm,求AC的长.
分析 (1)连接OD,由OB=OD和角平分线性质得出∠ODB=∠DBC.推出OD∥BC,得出∠ADO=∠C=90°,根据切线的判定推出即可;
(2)由OD∥BC得△AOD∽△ABC,得出$\frac{OD}{BC}$=$\frac{OA}{AB}$,求得OA,进一步求得AB,然后利用勾股定理即可求出AC的长.
解答 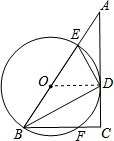 (1)证明:连接OD,
(1)证明:连接OD,
∵DE⊥DB,⊙O是△BDE的外接圆,
∴BE是⊙O的直径.
∵OB=OD,
∴∠OBD=∠ODB,
∵BD平分∠ABC,
∴∠OBD=∠DBC.
∴∠ODB=∠DBC.
∴OD∥BC,
∴∠ADO=∠C=90°,即OD⊥AC.
又∵点D在⊙O上,
∴AC是⊙O的切线.
(2)解:∵OD∥BC,
∴△AOD∽△ABC,
∴$\frac{OD}{BC}$=$\frac{OA}{AB}$,
∵⊙O的半径为5cm,BC=8cm,
∴$\frac{5}{8}$=$\frac{OA}{OA+5}$,
解得:OA=$\frac{25}{3}$cm.
∴AB=5+$\frac{25}{3}$=$\frac{40}{3}$ cm.
在Rt△ACB中,由勾股定理得:AC=$\sqrt{A{B}^{2}-B{C}^{2}}$=$\frac{32}{3}$.
点评 此题考查了切线的判定,相似三角形的判定与性质以及勾股定理的应用,熟练掌握切线的判定方法是解本题的关键.

练习册系列答案
相关题目
20.已知y是x的一次函数,函数y与自变量x的部分对应值如表,
点(x1,y1),(x2,y2)在该函数的图象上.若x1>x2,则y1<y2.
| x | … | -2 | -1 | 0 | 1 | 2 | … |
| y | … | 10 | 8 | 6 | 4 | 2 | … |
17. 如图,转盘中四个扇形的面积都相等.小明随意转动转盘2次,当转盘停止转动时,二次指针所指向数字的积为偶数的概率为( )
如图,转盘中四个扇形的面积都相等.小明随意转动转盘2次,当转盘停止转动时,二次指针所指向数字的积为偶数的概率为( )
 如图,转盘中四个扇形的面积都相等.小明随意转动转盘2次,当转盘停止转动时,二次指针所指向数字的积为偶数的概率为( )
如图,转盘中四个扇形的面积都相等.小明随意转动转盘2次,当转盘停止转动时,二次指针所指向数字的积为偶数的概率为( )| A. | $\frac{3}{4}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{2}$ | D. | $\frac{5}{6}$ |
1.对于二次函数y=(x-1)2+2的图象,下列说法正确的是( )
| A. | 开口向下 | B. | 顶点坐标是(1,2) | C. | 对称轴是x=-1 | D. | 与x轴有两个交点 |

 若有理数a、b、c在数轴上的位置如图所示,则化简:|a|+|a-b|-|c+b|=2a+c.
若有理数a、b、c在数轴上的位置如图所示,则化简:|a|+|a-b|-|c+b|=2a+c. 如图,OA⊥OB,∠BOC=28°,OD平分∠AOC,则∠BOD的度数是31°.
如图,OA⊥OB,∠BOC=28°,OD平分∠AOC,则∠BOD的度数是31°.