题目内容
如图,在直角坐标系中,四边形ABCD是正方形,A(1,-1)、B(-1,-1)、C(-1,1)、D(1, 1).曲线AA A
A A
A …叫做“正方形的渐开线”,其中
…叫做“正方形的渐开线”,其中 、
、 、
、 …的圆心依次是点B、C、D、A循环,则点A
…的圆心依次是点B、C、D、A循环,则点A 的坐标是 .
的坐标是 .

(-4021,1).
【解析】
试题分析:先分别求出A1的坐标是(-1,-3),A2的坐标是(-5,1),A3的坐标是(1,7),A4的坐标是(9,-1),从中找出规律,依规律计算即可.
试题解析:从图中可以看出A1的坐标是(-1,-3)
A2的坐标是(-5,1)
A3的坐标是(1,7)
A4的坐标是(9,-1)
2010÷4=502…2
∴点A2010的坐标是A2的坐标循环后的点.
依次循环则A2010的坐标在y轴上的是1,
x轴上的坐标是可以用n=-(1+2n)(n为自然数)表示.
那么A2010实际上是当n=2010时的数,所以-(1+2×2010)=-4021.
A2010的坐标是(-4021,1).
考点:1.正方形的性质;2.坐标与图形性质.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案
相关题目




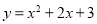 绕着它与
绕着它与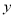 轴的交点旋转180°,所得抛物线的解析式是( ).
轴的交点旋转180°,所得抛物线的解析式是( ).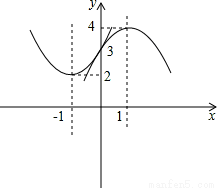
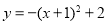 B.
B.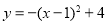
 D.
D.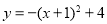
 中,
中, ,
, ,
, ,
, 分别为边
分别为边 的中点,将
的中点,将 绕点
绕点 顺时针旋转
顺时针旋转 到
到 的位置,则整个旋转过程中线段
的位置,则整个旋转过程中线段 所扫过部分的面积(即阴影部分面积)为( )
所扫过部分的面积(即阴影部分面积)为( )
 B.
B. C.
C. D.
D.
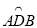 的中点,C,D在直径AB的两侧,若在⊙O内存在点E,使AE=AD,CB=CE.
的中点,C,D在直径AB的两侧,若在⊙O内存在点E,使AE=AD,CB=CE.
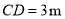 ,标杆与旗杆
,标杆与旗杆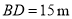 ,人的眼睛与地面的高度
,人的眼睛与地面的高度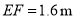 ,人与标杆
,人与标杆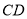 的水平距离
的水平距离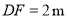 ,人的
,人的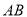 的高度.
的高度.