题目内容
如图,在□ABCD中,E,F分别为边AB,CD的中点,连结DE,BF,BD.

(1)求证:△ADE≌△CBF.
(2)若AD⊥BD,则四边形BFDE是什么特殊四边形?请证明你的结论.
(1)证明见解析;(2)菱形.理由见解析.
【解析】
试题分析:(1)根据题中已知条件不难得出,AD=BC,∠A=∠C,E、F分别为边AB、CD的中点,那么AE=CF,这样就具备了全等三角形判定中的SAS,由此可得出△AED≌△CFB.
(2)直角三角形ADB中,DE是斜边上的中线,因此DE=BE,又由DE=BF,FD∥BE那么可得出四边形BFDE是个菱形.
试题解析:(1)证明:在平行四边形ABCD中,∠A=∠C,AD=BC,
∵E、F分别为AB、CD的中点,
∴AE=CF.
在△AED和△CFB中,

∴△AED≌△CFB(SAS);
(2)【解析】
若AD⊥BD,则四边形BFDE是菱形.
证明:∵AD⊥BD,
∴△ABD是直角三角形,且∠ADB=90°.
∵E是AB的中点,
∴DE= AB=BE.
AB=BE.
∵在ABCD中,E,F分别为边AB,CD的中点,
∴EB∥DF且EB=DF,
∴四边形BFDE是平行四边形.
∴四边形BFDE是菱形.
考点:1.全等三角形的判定;2.平行四边形的性质;3.菱形的判定.

练习册系列答案
相关题目
 ,
, D、4、5、6
D、4、5、6 cm.
cm.
 的长(结果保留
的长(结果保留 ).
). ,动点P从点D出发,沿射线DA的方向以每秒2个单位长的速度运动,动点Q从点C出发,在线段CB上以每秒一个单位长的速度向点B运动,点P,Q分别从点D,C同时出发,当点Q运动到点B时,点P随之停止运动.设运动的时间为t(秒).
,动点P从点D出发,沿射线DA的方向以每秒2个单位长的速度运动,动点Q从点C出发,在线段CB上以每秒一个单位长的速度向点B运动,点P,Q分别从点D,C同时出发,当点Q运动到点B时,点P随之停止运动.设运动的时间为t(秒).
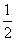 AC长为半径画弧相交于点M、N,连接MN,与AC、BC分别交于点D、E,连接AE.
AC长为半径画弧相交于点M、N,连接MN,与AC、BC分别交于点D、E,连接AE.
 A
A A
A …叫做“正方形的渐开线”,其中
…叫做“正方形的渐开线”,其中 、
、 、
、 …的圆心依次是点B、C、D、A循环,则点A
…的圆心依次是点B、C、D、A循环,则点A 的坐标是 .
的坐标是 .
 x2+bx经过点A(4,0).设点C(1,-3),请在抛物线的对称轴上确定一点D,使得
x2+bx经过点A(4,0).设点C(1,-3),请在抛物线的对称轴上确定一点D,使得 的值最大,则D点的坐标为_____.
的值最大,则D点的坐标为_____.