题目内容
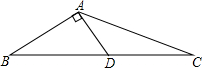 如图,在△ABC中,AD是BC边上的中线,且AD⊥AB,AB=3,AC=5,求AD的长.
如图,在△ABC中,AD是BC边上的中线,且AD⊥AB,AB=3,AC=5,求AD的长.考点:勾股定理
专题:
分析:延长AD至E,使DE=AD,连接BE.根据SAS证明△ACD≌△EBD,得BE=CA,AD=ED,再根据勾股定理即可求解.
解答: 解:延长AD至E,使DE=AD,连接BE.
解:延长AD至E,使DE=AD,连接BE.
∵AD是BC边上的中线,
∴CD=BD,
在△ACD与△EBD中,
,
∴△ACD≌△EBD(SAS),
∴BE=CA,AD=ED,
∵AD⊥AB,
∴△ABE是直角三角形,
在Rt△ABE中,AB=3,BE=AC=5,
∴AE=4,
∴AD=2.
故AD的长是2.
 解:延长AD至E,使DE=AD,连接BE.
解:延长AD至E,使DE=AD,连接BE.∵AD是BC边上的中线,
∴CD=BD,
在△ACD与△EBD中,
|
∴△ACD≌△EBD(SAS),
∴BE=CA,AD=ED,
∵AD⊥AB,
∴△ABE是直角三角形,
在Rt△ABE中,AB=3,BE=AC=5,
∴AE=4,
∴AD=2.
故AD的长是2.
点评:此题综合运用了全等三角形的判定和性质、勾股定理.注意:倍长中线是常见的辅助线之一.

练习册系列答案
相关题目
等腰三角形一腰上的高与另一腰的夹角为40°,则它的底角度数是( )
| A、65° | B、65°或25° |
| C、25° | D、50° |
数据1556000用科学记数法表示为( )
| A、1.556×107 |
| B、0.1556×108 |
| C、15.56×105 |
| D、1.556×106 |
 如图,大圆的半径是R,小圆面积是大圆面积的
如图,大圆的半径是R,小圆面积是大圆面积的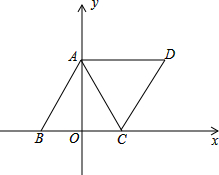 如图,在等边△ABC中,B(-1,0)、C(1,0),以底边BC的垂直平分线和BC所在直线建立平面直角坐标系,把△ABC绕着点C顺时针旋转60°的得到△DEF,(旋转后D与A、E与B、F与C对应)
如图,在等边△ABC中,B(-1,0)、C(1,0),以底边BC的垂直平分线和BC所在直线建立平面直角坐标系,把△ABC绕着点C顺时针旋转60°的得到△DEF,(旋转后D与A、E与B、F与C对应)