题目内容
若x1,x2是关于x的方程x2+bx+c=0的两个实数根,且满足|x1|+2|x2|=|c|+2,则称方程x2+bx+c=0为“T系二次方程”.如方程x2+2x=0,x2+5x+6=0,x2-6x-16=0,x2+4x+4=0都是“T系二次方程”.是否存在实数b,使得关于x的方程x2+bx+b+
=0是“T系二次方程”,并说明理由.
| 2 |
考点:一元二次方程的应用
专题:
分析:根据x=-2时,求出b=4+
,再把b的值代入x2+bx+b+
=0,求出x的值,再分别求出|x1|+2|x2|和|c|+2的值,即可得出答案.
| 2 |
| 2 |
解答:解:当x=-2时,
由方程x2+bx+b+
=0得到:4-2b+b+
=0,
则b=4+
,
x2+(4+
)x+4+
+
=0,
解得:x1=-2,x2=-2-
,
则|x1|+2|x2|=2+4+2
=6+2
,
|c|+2=4+2
+2=6+2
,
即当b=4+
时,方程x2+bx+b+
=0是“T系二次方程”.
由方程x2+bx+b+
| 2 |
| 2 |
则b=4+
| 2 |
x2+(4+
| 2 |
| 2 |
| 2 |
解得:x1=-2,x2=-2-
| 2 |
则|x1|+2|x2|=2+4+2
| 2 |
| 2 |
|c|+2=4+2
| 2 |
| 2 |
即当b=4+
| 2 |
| 2 |
点评:此题考查了一元二次方程的应用,关键是读懂题意,根据题目中的数量关系列出方程,再求解.

练习册系列答案
相关题目
下列计算正确的是( )
| A、(a+b)2=a2+b2 |
| B、ambn=(ab)m+n |
| C、(ab)n=anbn |
| D、(ab)mn=ambn |
 如图,弦AB⊥OC,垂足为点C,连接OA,若OC=2,AB=4,则OA等于( )
如图,弦AB⊥OC,垂足为点C,连接OA,若OC=2,AB=4,则OA等于( )A、2
| ||
B、2
| ||
C、3
| ||
D、2
|
代数式-
,
,x+y,
,
,
,
中是分式的有( )
| 3x |
| 2 |
| 4 |
| x-y |
| x2+1 |
| π |
| 7 |
| 8 |
| 5b |
| 3a |
| x2 |
| x |
| A、1个 | B、2个 | C、3个 | D、4个 |
二次根式
有意义时,x的取值范围是( )
| x+3 |
| A、x≥-3 | B、x>-3 |
| C、x≤-3 | D、x≠-3 |
 二次函数y=ax2+bx+c(a≠0)的图象如图所示,根据图象解答下列问题:
二次函数y=ax2+bx+c(a≠0)的图象如图所示,根据图象解答下列问题: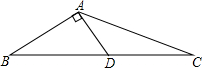 如图,在△ABC中,AD是BC边上的中线,且AD⊥AB,AB=3,AC=5,求AD的长.
如图,在△ABC中,AD是BC边上的中线,且AD⊥AB,AB=3,AC=5,求AD的长.