题目内容
17.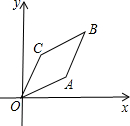 如图,在菱形OABC中,点A的坐标是(2,1),点B的横坐标是3,则点C的坐标是(1,2).
如图,在菱形OABC中,点A的坐标是(2,1),点B的横坐标是3,则点C的坐标是(1,2).
分析 作AD⊥x轴于D,BF⊥x轴于F,AE⊥BF于E,BG⊥y轴于H,CG⊥BH于G,CM⊥Y轴于M,则四边形BHOF是矩形,四边形ADFE是矩形,四边形GHMC是矩形,证明Rt△ABE≌Rt△AOD,得出BE=OD=2,求出BF=3,同理可证:△CBG≌△AOD,得出CG=AD=1,BG=OD=2,得出HM=1,OM=2,即可得出结果.
解答 解:作AD⊥x轴于D,BF⊥x轴于F,AE⊥BF于E,BG⊥y轴于H,CG⊥BH于G,CM⊥Y轴于M,如图所示: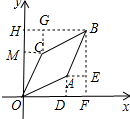 则四边形BHOF是矩形,四边形ADFE是矩形,四边形GHMC是矩形,∠ADO=∠AEB=∠CGB=∠CMO=90°,
则四边形BHOF是矩形,四边形ADFE是矩形,四边形GHMC是矩形,∠ADO=∠AEB=∠CGB=∠CMO=90°,
∵点A的坐标是(2,1),点B的横坐标是3,
∴OD=2,EF=AD=1,BH=3,
∴AE=1,
∴AE=AD,
∵四边形OABC是菱形,
∴OA=AB=BC=OC,
在Rt△ABE和Rt△AOD中,$\left\{\begin{array}{l}{AB=OA}\\{AE=AD}\end{array}\right.$,
∴Rt△ABE≌Rt△AOD(HL),
∴BE=OD=2,
∴BF=3=BH,
同理可证:△CBG≌△AOD,
∴CG=AD=1,BG=OD=2,
∴HM=1,OM=3-1=2,
∴C(1,2);
故答案为:(1,2).
点评 本题考查了菱形的性质、坐标与图形性质、全等三角形的判定与性质、矩形的判定与性质;熟练掌握菱形的性质,证明三角形全等是解决问题的关键.

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目
8.从青岛到济南有南线和北线两条高速公路,南线全长400千米,北线全长320千米.甲、乙两辆客车分别有南线和北线从青岛同时驶往济南,已知客车甲在南线高速公路上行驶的平均速度比客车乙在北线高速公路上快20千米/小时,两车恰好同时到达济南.若设客车乙从青岛到济南的平均速度是x千米/小时,则根据题意可得方程( )
| A. | $\frac{400}{x-20}$=$\frac{320}{x}$ | B. | $\frac{400}{x+20}$=$\frac{320}{x}$ | C. | $\frac{400}{x}$+20=$\frac{320}{x}$ | D. | $\frac{400}{x}$=$\frac{320}{x+20}$ |
5.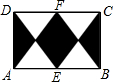 如图,一个矩形区域ABCD,点E、F分别是AB、DC的中点,则一只蝴蝶落在阴影部分的概率是( )
如图,一个矩形区域ABCD,点E、F分别是AB、DC的中点,则一只蝴蝶落在阴影部分的概率是( )
 如图,一个矩形区域ABCD,点E、F分别是AB、DC的中点,则一只蝴蝶落在阴影部分的概率是( )
如图,一个矩形区域ABCD,点E、F分别是AB、DC的中点,则一只蝴蝶落在阴影部分的概率是( )| A. | $\frac{1}{4}$ | B. | $\frac{17}{38}$ | C. | $\frac{2}{5}$ | D. | $\frac{1}{2}$ |
12.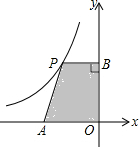 如图,平面直角坐标系中,点A是x轴负半轴上一个定点,点P是函数$y=-\frac{4}{x}$(x<0)上一个动点,PB⊥y轴于点B,当点P的横坐标逐渐增大时,四边形OAPB的面积将会( )
如图,平面直角坐标系中,点A是x轴负半轴上一个定点,点P是函数$y=-\frac{4}{x}$(x<0)上一个动点,PB⊥y轴于点B,当点P的横坐标逐渐增大时,四边形OAPB的面积将会( )
 如图,平面直角坐标系中,点A是x轴负半轴上一个定点,点P是函数$y=-\frac{4}{x}$(x<0)上一个动点,PB⊥y轴于点B,当点P的横坐标逐渐增大时,四边形OAPB的面积将会( )
如图,平面直角坐标系中,点A是x轴负半轴上一个定点,点P是函数$y=-\frac{4}{x}$(x<0)上一个动点,PB⊥y轴于点B,当点P的横坐标逐渐增大时,四边形OAPB的面积将会( )| A. | 逐渐增大 | B. | 先减后增 | C. | 逐渐减小 | D. | 先增后减 |
7.在2014年“汕头市初中毕业升学体育考试”测试中,参加男子掷实心球的10名考生的成绩记录如下(单位:米):7.5、6.5、8.2、7.8、8.8、8.2、8.6、8.2、8.5、9.5,则该组数据的众数、中位数、平均数依次分别是( )
| A. | 8.2、8.0、7.5 | B. | 8.2、8.5、8.1 | C. | 8.2、8.2、8.15 | D. | 8.2、8.2、8.18 |