题目内容
12．
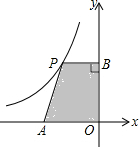如图，平面直角坐标系中，点A是x轴负半轴上一个定点，点P是函数$y=-\frac{4}{x}$（x＜0）上一个动点，PB⊥y轴于点B，当点P的横坐标逐渐增大时，四边形OAPB的面积将会（ ）| A． | 逐渐增大 | B． | 先减后增 | C． | 逐渐减小 | D． | 先增后减 |
分析 由双曲线y=-$\frac{4}{x}$（x＞0）设出点P的坐标，运用坐标表示出四边形OAPB的面积函数关系式即可判定．
解答 解：设点P的坐标为（x，-$\frac{4}{x}$），
∵PB⊥y轴于点B，点A是x轴正半轴上的一个定点，
∴四边形OAPB是个直角梯形，
∴四边形OAPB的面积=$\frac{1}{2}$（PB+AO）•BO=$\frac{1}{2}$（-x+AO）•-$\frac{4}{x}$=2-$\frac{2OA}{x}$，
∵AO是定值，
∴四边形OAPB的面积是个增函数，即点P的横坐标逐渐增大时四边形OAPB的面积逐渐增大．
故选A．
点评 本题主要考查了反比例函数系数k的几何意义，解题的关键是运用点的坐标求出四边形OAPB的面积的函数关系式．
练习册系列答案
相关题目
2．
某校八年级全体男同学参加了跳绳比赛，从中随机抽取某班男同学的跳绳成绩，制作了如下频数分布表：
根据上面统计信息，解答下列问题：
（1）不全频数分布直方图．
（2）班级准备对跳绳成绩优秀的男同学进行奖励，奖励人数占班级男同学的20%，该班张辉同学的成绩为140个，通过计算判断张辉能否获得奖励．
（3）八年级共有200名男同学，若规定男同学的跳绳成绩在120个以上（含120个）为合格，估计该校八年级男同学成绩合格的人数．
某校八年级全体男同学参加了跳绳比赛，从中随机抽取某班男同学的跳绳成绩，制作了如下频数分布表：| 组别 | 99.5-109.5 | 109.5-119.5 | 119.5-129.5 | 129.5-139.5 | 139.5-149.5 | 149.5-159.5 |
| 频数 | 2 | 4 | 8 | 7 | 3 | 1 |
（1）不全频数分布直方图．
（2）班级准备对跳绳成绩优秀的男同学进行奖励，奖励人数占班级男同学的20%，该班张辉同学的成绩为140个，通过计算判断张辉能否获得奖励．
（3）八年级共有200名男同学，若规定男同学的跳绳成绩在120个以上（含120个）为合格，估计该校八年级男同学成绩合格的人数．
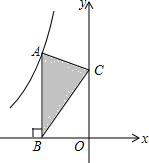如图，点A是反比例函数y=$\frac{k}{x}$的图象上的一点，过点A作AB⊥x轴，垂足为B，点C为y轴上的一点，连接AC、BC，若△ABC的面积为3，则k的值是-6．
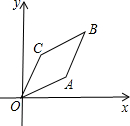如图，在菱形OABC中，点A的坐标是（2，1），点B的横坐标是3，则点C的坐标是（1，2）．
4．9的算术平方根是（ ）
| A． | ±3 | B． | -3 | C． | 3 | D． | ±81 |
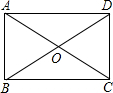如图，矩形ABCD的对角线AC、BD交于点O，∠AOB=60°，AB=3，求BD的长．