题目内容
9.若关于x的一元二次方程x2-2mx-m-$\frac{1}{4}$=0有两个相等的实数根,则m的值为( )| A. | m=$\frac{1}{2}$ | B. | m=-$\frac{1}{2}$ | C. | m=2 | D. | m=-2 |
分析 由方程有两个相等的实数根可知b2-4ac=0,套入数据可得(2m+1)2=0,解该方程即可得出m的值.
解答 解:∵关于x的一元二次方程x2-2mx-m-$\frac{1}{4}$=0有两个相等的实数根,
∴b2-4ac=(-2m)2-4×1×(-m-$\frac{1}{4}$)=0,即(2m+1)2=0,
解得:m=-$\frac{1}{2}$.
故选B.
点评 本题考查了根的判别式,解题的关键是找出(2m+1)2=0.本题属于基础题,难度不大,解决该题型题目时,根据根的个数结合根的判别式得出关于m的一元二次方程是关键.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
4.一个长方形在平面直角坐标系中,若其三个顶点的坐标分别为(-3,-2),(2,-2),(2,1),则第四个顶点为( )
| A. | (2,-5) | B. | (2,2) | C. | (3,1) | D. | (-3,1) |
18.$\frac{\sqrt{{x}^{2}-9}}{\sqrt{x-3}}$有意义,则x的取值为( )
| A. | x>3 | B. | x>3或x<-3 | C. | x≧3 | D. | x≧-3 |
19.下列语句中,是真命题的是( )
| A. | 任何实数都有相反数、倒数 | |
| B. | 过一点有且只有一条直线与已知直线平行 | |
| C. | 在同一平面内不相交的两条直线叫做平行线 | |
| D. | 两条直线被第三条直线所截,同位角相等 |
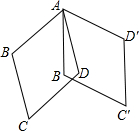 如图,菱形ABCD中,∠B=120°,AB=2,将图中的菱形ABCD绕点A沿逆时针方向旋转,得菱形AB′C′D′,若∠BAD′=110°,在旋转的过程中,点C经过的路线长为$\frac{{5\sqrt{3}}}{9}π$.
如图,菱形ABCD中,∠B=120°,AB=2,将图中的菱形ABCD绕点A沿逆时针方向旋转,得菱形AB′C′D′,若∠BAD′=110°,在旋转的过程中,点C经过的路线长为$\frac{{5\sqrt{3}}}{9}π$. 如图,AC与BD相交于点O,AO=DO,∠1=∠2,求证:AB=CD.
如图,AC与BD相交于点O,AO=DO,∠1=∠2,求证:AB=CD.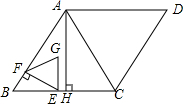 如图,在菱形ABCD中,AB=6,∠ABC=60°,AH⊥BC于点H.动点E从点B出发,沿线段BC向点C以每秒2个单位长度的速度运动.过点E作EF⊥AB,垂足为点F.点E出发后,以EF为边向上作等边三角形EFG,设点E的运动时间为t秒,△EFG和△AHC的重合部分面积为S.
如图,在菱形ABCD中,AB=6,∠ABC=60°,AH⊥BC于点H.动点E从点B出发,沿线段BC向点C以每秒2个单位长度的速度运动.过点E作EF⊥AB,垂足为点F.点E出发后,以EF为边向上作等边三角形EFG,设点E的运动时间为t秒,△EFG和△AHC的重合部分面积为S.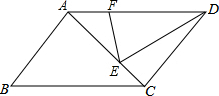 如图,在平行四边形ABCD中,E在AC上,AE=2EC,F在AD上,DF=2AF,如果△DEF的面积为2,则平行四边形ABCD的面积为( )
如图,在平行四边形ABCD中,E在AC上,AE=2EC,F在AD上,DF=2AF,如果△DEF的面积为2,则平行四边形ABCD的面积为( )