题目内容
4.一个长方形在平面直角坐标系中,若其三个顶点的坐标分别为(-3,-2),(2,-2),(2,1),则第四个顶点为( )| A. | (2,-5) | B. | (2,2) | C. | (3,1) | D. | (-3,1) |
分析 设点D的坐标为(m,n),由长方形的性质可以得出“DC=AB,AD=BC”,由DC=AB可得出关于m的一元一次方程,由AD=BC可得出关于n的一元一次方程,解方程即可得出点D的坐标.
解答 解:依照题意画出图形,如图所示.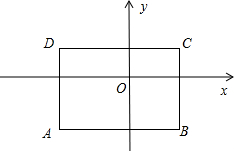
设点D的坐标为(m,n),
∵点A(-3,-2),B(2,-2),C(2,1),
AB=2-(-3)=5,DC=AB=5=2-m=5,
解得:m=-3;
BC=1-(-2)=3,AD=BC=3=n-(-2),
解得:n=1.
∴点D的坐标为(-3,1).
故选D.
点评 本题考查了坐标系中点的意义以及长方形的性质,解题的关键是分别得出关于m、n的一元一次方程.本题属于基础题,难度不大,解决该题型题目时,依照题意画出图形,再根据图形的性质即可得出结论.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
15.小马虎在做作业,不小心将方程中的一个常数污染了,被污染的方程是2(x-3)-•=x+1,怎么办呢?他想了想便翻看书后的答案,方程的解是x=9,请问这个被污染的常数是( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
9.若关于x的一元二次方程x2-2mx-m-$\frac{1}{4}$=0有两个相等的实数根,则m的值为( )
| A. | m=$\frac{1}{2}$ | B. | m=-$\frac{1}{2}$ | C. | m=2 | D. | m=-2 |
16.下列从左到右的变形中,属于因式分解的是( )
| A. | (x+y)(x-2y)=x2-x+y2 | B. | (a-b)2=(a-b)(a-b) | C. | 3x2-x=x(3x-1) | D. | m2-n2=(m-n)2 |
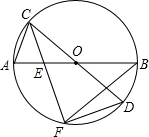 如图,AB、CD为⊙O的直径,E为OA的中点,直线CE交⊙O于另一点F,连接DF,若⊙O的半径为4,DF=$\sqrt{15}$,CE<EF
如图,AB、CD为⊙O的直径,E为OA的中点,直线CE交⊙O于另一点F,连接DF,若⊙O的半径为4,DF=$\sqrt{15}$,CE<EF 如图,若直线a∥b,那么∠x=64度.
如图,若直线a∥b,那么∠x=64度.