Question

1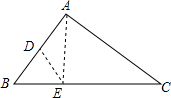．如图，△ABC中，∠C=45°，点D在AB上，点E在BC上，若AD=DB=DE，AE=1，则AC的长为$\sqrt{2}$．

Answer 1

分析 根据等边对等角和三角形内角和定理得：∠DEB+∠AED=90°，所以∠AEC=90°，由∠C=45°，可知△AEC是等腰三角形，根据勾股定理求AC的长．

解答 解：∵AD=DB=DE，
∴∠DAE=∠AED，∠B=∠DEB，
∵∠B+∠DEB+∠AED+∠DAE=180°，
∴2∠DEB+2∠AED=180°，
∴∠DEB+∠AED=90°，
∴∠AEC=90°，
∵∠C=45°，
∴△AEC是等腰三角形，
∴AE=EC=1，
∴AC=$\sqrt{2}$，
故答案为：$\sqrt{2}$．

点评 本题考查了等腰直角三角形的性质和判定、勾股定理、等腰三角形的性质，属于基础题，本题的关键是根据等边对等角证得∠AEC=90°是关键．