题目内容
10.将平面直角坐标系中的点P(m-2,2m+1)向左平移1个单位后位于第二象限,则m的取值范围是( )| A. | 0<m<2 | B. | -0.5<m<2 | C. | -0.5<m<1 | D. | -0.5<m<3 |
分析 关键是表示出向左平移1个单位后可得P(m-2-1,2m+1),再根据第二象限内点的坐标符号可得$\left\{\begin{array}{l}{m-3<0}\\{2m+1>0}\end{array}\right.$,再解不等式组即可.
解答 解:∵点P(-2m,2m+1),
∴向左平移1个单位后可得P(m-2-1,2m+1),
即(m-3,2m+1),
∵位于第二象限,
∴$\left\{\begin{array}{l}{m-3<0}\\{2m+1>0}\end{array}\right.$,
解得:-0.5<m<3,
故选:D.
点评 此题主要考查了坐标与图形变化-平移,以及平面直角坐标系中点的坐标符号,关键是掌握横坐标,右移加,左移减;纵坐标,上移加,下移减.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
1.下列各数2π,-5,0.$\stackrel{•}{4}$,-3.14,0中,负数有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
18.在Rt△ABC中,∠C=90°,∠A的对边为a,∠B的对边为b,且满足a2-ab-b2=0,则tanA=( )
| A. | 1 | B. | $\frac{1+\sqrt{5}}{2}$ | C. | $\frac{1-\sqrt{5}}{2}$ | D. | $\frac{1±\sqrt{5}}{2}$ |
19.下列多项式中,各项系数的积是30的是( )
| A. | -x2+5x+6 | B. | 2x2+2x-5 | C. | $\frac{{4{x^2}-20x-3}}{2}$ | D. | -32x+$\frac{2}{3}$y+5z |
 如图,AB∥CD,AC、BC相交于点E,∠B=52°,求∠C.
如图,AB∥CD,AC、BC相交于点E,∠B=52°,求∠C.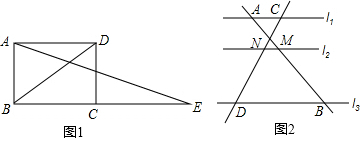
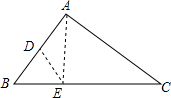 如图,△ABC中,∠C=45°,点D在AB上,点E在BC上,若AD=DB=DE,AE=1,则AC的长为$\sqrt{2}$.
如图,△ABC中,∠C=45°,点D在AB上,点E在BC上,若AD=DB=DE,AE=1,则AC的长为$\sqrt{2}$.