题目内容
小明对直角三角形很感兴趣.△ABC中,∠ACB=90°,D是AB上任意一点,连接DC,作DE⊥DC,EA⊥AC,DE与AE交于点E.请你跟着他一起解决下列问题:
(1)如图1,若△ABC是等腰直角三角形,则DE,DC有什么数量关系?请给出证明.
(2)如果换一个直角三角形,如图2,∠CBA=30°,则DE,DC又有什么数量关系?请给出证明.
(3)由(1)、(2)这两种特殊情况,小明提出问题:如果直角三角形ABC中,BC=mAC,那DE,DC有什么数量关系?请给出证明.
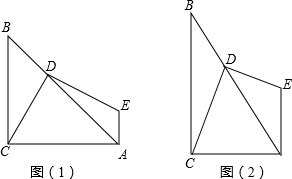
(1)如图1,若△ABC是等腰直角三角形,则DE,DC有什么数量关系?请给出证明.
(2)如果换一个直角三角形,如图2,∠CBA=30°,则DE,DC又有什么数量关系?请给出证明.
(3)由(1)、(2)这两种特殊情况,小明提出问题:如果直角三角形ABC中,BC=mAC,那DE,DC有什么数量关系?请给出证明.

考点:相似三角形的判定与性质,全等三角形的判定与性质,等腰直角三角形
专题:
分析:(1)由条件可证得△CDF∽△EDG,且相似比为1,所以可得出DC=DE;
(2)由(1)的方法可证得△CDF∽△EDG,且相似比为
,所以可得DC=
DE;
(3)同(2)的方法可证得△CDF∽△EDG,且相似比为m,所以可得DC=mDE.
(2)由(1)的方法可证得△CDF∽△EDG,且相似比为
| 3 |
| 3 |
(3)同(2)的方法可证得△CDF∽△EDG,且相似比为m,所以可得DC=mDE.
解答: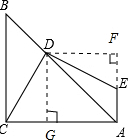 解:(1)DE=DC.过点D作DG⊥AC于点G,DF⊥AE于点F,由EA⊥AC,
解:(1)DE=DC.过点D作DG⊥AC于点G,DF⊥AE于点F,由EA⊥AC,
可知四边形AGDF为矩形,
所以DG=FA.而DF∥BC,
所以DF=AF,即DG=DF;
又因为DE⊥DC,
所以∠CDE-∠EDF=∠FDG-∠EDF,
即∠CDF=∠EDG,
所以△CDF∽△EDG,
=
=1,
即DE=DC;
(2)DC=
DE.同理,由∠CDF=∠EDG,可证△CDF∽△EDG,
=
=
=
=
,所以DC=
DE;
(3)DC=mDE.同理,由∠CDF=∠EDG,可证△CDF∽△EDG,
=
=
=
=m,所以DC=mDE.
 解:(1)DE=DC.过点D作DG⊥AC于点G,DF⊥AE于点F,由EA⊥AC,
解:(1)DE=DC.过点D作DG⊥AC于点G,DF⊥AE于点F,由EA⊥AC,可知四边形AGDF为矩形,
所以DG=FA.而DF∥BC,
所以DF=AF,即DG=DF;
又因为DE⊥DC,
所以∠CDE-∠EDF=∠FDG-∠EDF,
即∠CDF=∠EDG,
所以△CDF∽△EDG,
| DC |
| DE |
| DF |
| DG |
即DE=DC;
(2)DC=
| 3 |
| DC |
| DE |
| DF |
| DG |
| DF |
| FA |
| BC |
| AC |
| 3 |
| 3 |
(3)DC=mDE.同理,由∠CDF=∠EDG,可证△CDF∽△EDG,
| DC |
| DE |
| DF |
| DG |
| DF |
| FA |
| BC |
| AC |
点评:本题主要考查相似三角形的判定和性质,掌握相似三角形的判定方法是解题的关键.

练习册系列答案
相关题目
下列各组数中是勾股数的一组是( )
| A、2、3、4 |
| B、4、5、6 |
| C、7、8、9 |
| D、9、40、41 |
 如图Rt△ABC中,D是CB延长线上一点,以AD为边作△ADE,连接BE,∠ABC=∠AED=∠ADE=α,求BE-BC与DC的关系.
如图Rt△ABC中,D是CB延长线上一点,以AD为边作△ADE,连接BE,∠ABC=∠AED=∠ADE=α,求BE-BC与DC的关系. 如图,梯形ABCD中,AD∥BC,∠ABC=90°,∠C=45°,BC=4,作DE⊥BC于点E,将△DEC沿直线DE折叠,点C落在CB的延长线上F处,DF交BC于点G.设AD=x,其中0<x<2.
如图,梯形ABCD中,AD∥BC,∠ABC=90°,∠C=45°,BC=4,作DE⊥BC于点E,将△DEC沿直线DE折叠,点C落在CB的延长线上F处,DF交BC于点G.设AD=x,其中0<x<2. 如图,在平面直角坐标系中,
如图,在平面直角坐标系中,