题目内容
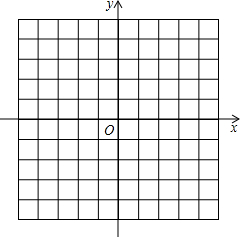 如图,在平面直角坐标系中,
如图,在平面直角坐标系中,(1)描出A(-4,3)、B(-1,0)、C(-2,3)三点.
(2)△ABC的面积是多少?
(3)作出△ABC关于y轴的对称图形.
考点:作图-轴对称变换
专题:
分析:(1)利用A,B,C各点坐标在平面坐标系中描出即可;
(2)利用三角形面积公式求出即可;
(3)利用关于y轴对称点的坐标性质进而得出答案.
(2)利用三角形面积公式求出即可;
(3)利用关于y轴对称点的坐标性质进而得出答案.
解答: 解:(1)如图所示:△ABC即为所求;
解:(1)如图所示:△ABC即为所求;
(2)△ABC的面积是:
×2×3=3;
(3)如图所示:△A′B′C′即为所求.
 解:(1)如图所示:△ABC即为所求;
解:(1)如图所示:△ABC即为所求;(2)△ABC的面积是:
| 1 |
| 2 |
(3)如图所示:△A′B′C′即为所求.
点评:此题主要考查了轴对称变换以及三角形面积求法,正确利用轴对称求出对应点坐标是解题关键.

练习册系列答案
相关题目
如果线段a、b、c、d是成比例线段且a=3,b=6,c=5,则d=( )
| A、8 | B、12 | C、10 | D、16 |
一台机器原价为100万元,如果每年的折旧率为x,两年后这台机器的价位为y万元,则y与x之间的函数关系为( )
| A、y=100(1-x)2 |
| B、y=100(1-x2) |
| C、y=100-x2 |
| D、y=100x2 |
 已知:如图,∠C=∠D=Rt∠,AC=AD.求证:
已知:如图,∠C=∠D=Rt∠,AC=AD.求证: 已知如图:点A(0,4),B(3,0),且∠1=∠2.则C点的坐标是
已知如图:点A(0,4),B(3,0),且∠1=∠2.则C点的坐标是 如图,一只蚂蚁从长、宽都是3,高是8的长方体纸箱的点A沿纸箱外表面爬到点B,那么它所行的最短路线的长是多少?
如图,一只蚂蚁从长、宽都是3,高是8的长方体纸箱的点A沿纸箱外表面爬到点B,那么它所行的最短路线的长是多少?