题目内容
 如图Rt△ABC中,D是CB延长线上一点,以AD为边作△ADE,连接BE,∠ABC=∠AED=∠ADE=α,求BE-BC与DC的关系.
如图Rt△ABC中,D是CB延长线上一点,以AD为边作△ADE,连接BE,∠ABC=∠AED=∠ADE=α,求BE-BC与DC的关系.考点:全等三角形的判定与性质
专题:
分析:过A作AF⊥BE于F,根据题意可求得△AEF≌△ADC,即可解题.
解答:解:过A作AF⊥BE于F,

∵∠ABC=∠AED=α,∠ABC+∠ABD=180°,
∴∠AED+∠ABD=180°,
∴A,B,D,E四点共圆,
∵∠ADE=∠ABE=α,
∴∠ABC=∠ABE,
∴BC=BF,
∵∠ABE=∠AED=α,
∴AD=AE,
在△AEF和△ADC中,
,
∴△AEF≌△ADC(AAS),
∴DC=EF,
∴BE=EF+BF=DC+BC,
∴BE-BC=DC.

∵∠ABC=∠AED=α,∠ABC+∠ABD=180°,
∴∠AED+∠ABD=180°,
∴A,B,D,E四点共圆,
∵∠ADE=∠ABE=α,
∴∠ABC=∠ABE,
∴BC=BF,
∵∠ABE=∠AED=α,
∴AD=AE,
在△AEF和△ADC中,
|
∴△AEF≌△ADC(AAS),
∴DC=EF,
∴BE=EF+BF=DC+BC,
∴BE-BC=DC.
点评:本题考查了全等三角形的判定,考查了全等三角形对应边相等的性质.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 一个几何体由几块大小相同的小立方体搭成,从上面观察这个几何体,看到的形状如图所示,其中小正方形中的数字表示在该位置小立方块的个数,请画出这个几何体从正面、左面观察的形状图.
一个几何体由几块大小相同的小立方体搭成,从上面观察这个几何体,看到的形状如图所示,其中小正方形中的数字表示在该位置小立方块的个数,请画出这个几何体从正面、左面观察的形状图.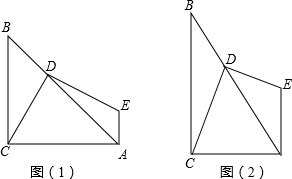
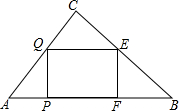 如图,在Rt△ABC中,∠C=90°,AC=30cm,BC=40m,矩形EFPQ的四个定点分别在三边上.设EF=xm,矩形EFPQD的面积为ym2,当x为何值时,y的值最大?最大值是多少?
如图,在Rt△ABC中,∠C=90°,AC=30cm,BC=40m,矩形EFPQ的四个定点分别在三边上.设EF=xm,矩形EFPQD的面积为ym2,当x为何值时,y的值最大?最大值是多少? 已知:如图,∠C=∠D=Rt∠,AC=AD.求证:
已知:如图,∠C=∠D=Rt∠,AC=AD.求证: 如图,一只蚂蚁从长、宽都是3,高是8的长方体纸箱的点A沿纸箱外表面爬到点B,那么它所行的最短路线的长是多少?
如图,一只蚂蚁从长、宽都是3,高是8的长方体纸箱的点A沿纸箱外表面爬到点B,那么它所行的最短路线的长是多少?