题目内容
 如图,已知⊙B与△ABD的边AD相切于点C,AD=10,AC=4,⊙B的半径为3.
如图,已知⊙B与△ABD的边AD相切于点C,AD=10,AC=4,⊙B的半径为3.(1)分别求出AB和BD的长.
(2)以点A为圆心画圆,当⊙A与⊙B相切时,求出⊙A的半径.
考点:切线的性质
专题:计算题
分析:(1)连接BC,由AD为圆B的切线,利用切线的性质得到BC垂直于AD,在直角三角形ABC中,利用勾股定理求出AB的长,在直角三角形BCD中,利用勾股定理求出BD的长即可;
(2)分两种情况考虑:当圆A与圆B外切;当圆A与圆B内切,分别求出圆A的半径即可.
(2)分两种情况考虑:当圆A与圆B外切;当圆A与圆B内切,分别求出圆A的半径即可.
解答: 解:(1)连接BC,
解:(1)连接BC,
∵AD为圆B的切线,
∴BC⊥AD,BC=r=3,
在Rt△ABC中,AC=4,BC=3,
根据勾股定理得:AB=
=5,
在Rt△BCD中,CD=AD-AC=10-4=6,BC=3,
根据勾股定理得:BD=
=3
;
(2)当圆A与圆B外切时,AB=r+R,即5=3+R,即R=2;
当圆A与圆B内切时,AB=R-r,即5=R-3,即R=8,
则圆A的半径为2或8.
 解:(1)连接BC,
解:(1)连接BC,∵AD为圆B的切线,
∴BC⊥AD,BC=r=3,
在Rt△ABC中,AC=4,BC=3,
根据勾股定理得:AB=
| AC2+BC2 |
在Rt△BCD中,CD=AD-AC=10-4=6,BC=3,
根据勾股定理得:BD=
| BC2+CD2 |
| 5 |
(2)当圆A与圆B外切时,AB=r+R,即5=3+R,即R=2;
当圆A与圆B内切时,AB=R-r,即5=R-3,即R=8,
则圆A的半径为2或8.
点评:此题考查了切线的性质,勾股定理,以及两圆相切的性质,熟练掌握切线的性质是解本题的关键.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
若a2=25,|b|=3,则a+b所有可能的值为( )
| A、8 | B、8或2 |
| C、8或-2 | D、±8或±2 |
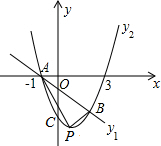 已知一次函数y1=-x+m与二次函数y2=ax2+bx-3的图象交于两点A(-1,0)、B(2,-3),且二次函数与y轴交于点C,P为抛物线顶点.求△ABP的面积.
已知一次函数y1=-x+m与二次函数y2=ax2+bx-3的图象交于两点A(-1,0)、B(2,-3),且二次函数与y轴交于点C,P为抛物线顶点.求△ABP的面积.