题目内容
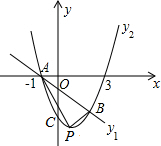 已知一次函数y1=-x+m与二次函数y2=ax2+bx-3的图象交于两点A(-1,0)、B(2,-3),且二次函数与y轴交于点C,P为抛物线顶点.求△ABP的面积.
已知一次函数y1=-x+m与二次函数y2=ax2+bx-3的图象交于两点A(-1,0)、B(2,-3),且二次函数与y轴交于点C,P为抛物线顶点.求△ABP的面积.考点:二次函数的性质
专题:
分析:把点A的坐标代入一次函数计算即可求出m,再把点A、B的坐标代入二次函数解析式,利用待定系数法求得解析式,然后把二次函数解析式整理成顶点式形式,然后写出顶点P的坐标,再求出对称轴与直线AB的交点坐标,然后利用三角形和梯形的面积公式列式计算即可得解;
解答:解:点A(-1,0)代入y1=-x+m得,1+m=0,
解得m=-1,
∵二次函数y2=ax2+bx-3经过A(-1,0)、B(2,-3),
∴
,
解得
,
所以二次函数的解析式为y2=x2-2x-3;
∵y2=x2-2x-3=(x-1)2-4,
∴顶点P坐标为(1,-4),
当x=1时,y1=-1-1=-2,
∴△ABP的面积=
×2×4+
×(3+4)×1+
×1×3-
×4×3=3.
解得m=-1,
∵二次函数y2=ax2+bx-3经过A(-1,0)、B(2,-3),
∴
|
解得
|
所以二次函数的解析式为y2=x2-2x-3;
∵y2=x2-2x-3=(x-1)2-4,
∴顶点P坐标为(1,-4),
当x=1时,y1=-1-1=-2,
∴△ABP的面积=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查了二次函数的性质:二次函数y=ax2+bx+c(a≠0)的图象为抛物线;对称轴为直线x=-
;抛物线与y轴的交点坐标为(0,c);当a>0时,抛物线开口向上,当x<-
时,y随x的增大而减小;x>-
时,y随x的增大而增大;x=-
时,y取得最小值
,即顶点是抛物线的最低点;当a<0时,抛物线开口向下,x<-
时,y随x的增大而增大;x>-
时,y随x的增大而减小;x=-
时,y取得最大值
,即顶点是抛物线的最高点.
| b |
| 2a |
| b |
| 2a |
| b |
| 2a |
| b |
| 2a |
| 4ac-b2 |
| 4a |
| b |
| 2a |
| b |
| 2a |
| b |
| 2a |
| 4ac-b2 |
| 4a |

练习册系列答案
 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
 如图,能判断直线AB∥CD的条件是( )
如图,能判断直线AB∥CD的条件是( )| A、∠1=∠2 |
| B、∠3=∠4 |
| C、∠1+∠3=180° |
| D、∠3+∠4=180° |
 如图,∠1的同位角是
如图,∠1的同位角是 如图,已知⊙B与△ABD的边AD相切于点C,AD=10,AC=4,⊙B的半径为3.
如图,已知⊙B与△ABD的边AD相切于点C,AD=10,AC=4,⊙B的半径为3.
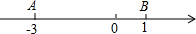 已知:如图数轴上两动点A、B原始位置所对应的数分别为-3、1,
已知:如图数轴上两动点A、B原始位置所对应的数分别为-3、1,