题目内容
15.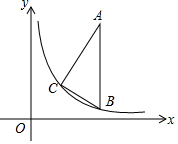 如图,在直角△ABC中,∠C=90°,∠A=30°,AB∥y轴,且AB=6,顶点B,C在反比例函数y=$\frac{k}{x}$(x>0)的图象上,且点B的横坐标为2$\sqrt{3}$,则k=$\sqrt{3}$.
如图,在直角△ABC中,∠C=90°,∠A=30°,AB∥y轴,且AB=6,顶点B,C在反比例函数y=$\frac{k}{x}$(x>0)的图象上,且点B的横坐标为2$\sqrt{3}$,则k=$\sqrt{3}$.
分析 作CD∥y轴,作BD⊥AB,交CD于D,解直角三角形求得CD=$\frac{1}{2}$BC=$\frac{3}{2}$,BD=$\sqrt{3}$BC=$\frac{3\sqrt{3}}{2}$,设点B的坐标为(2$\sqrt{3}$,m),则C(2$\sqrt{3}$-$\frac{3\sqrt{3}}{2}$,m+$\frac{3}{2}$),再根据点B、C在反比例函数图象上,即可得出关于m、k的二元一次方程组,解方程组即可得出结论.
解答 解:作CD∥y轴,作BD⊥AB,交CD于D,
∵AB∥y轴,
∴CD∥AB,
∴BD⊥CD,
∵∠ACB=90°,∠A=30°,
∴BC=$\frac{1}{2}$AB=3,∠ABC=60°,
∴∠CBD=30°,
∴CD=$\frac{1}{2}$BC=$\frac{3}{2}$,BD=$\sqrt{3}$BC=$\frac{3\sqrt{3}}{2}$,
设点B的坐标为(2$\sqrt{3}$,m),则C(2$\sqrt{3}$-$\frac{3\sqrt{3}}{2}$,m+$\frac{3}{2}$),
∵点B、C在反比例函数y=$\frac{k}{x}$(x>0)的图象上,
∴k=2$\sqrt{3}$m=$\frac{\sqrt{3}}{2}$•(m+$\frac{3}{2}$),
解得m=$\frac{1}{2}$,
∴k=2$\sqrt{3}$×$\frac{1}{2}$=$\sqrt{3}$;
故答案为:$\sqrt{3}$.
点评 本题考查了反比例函数图象上点的坐标特征,解题的关键是找出关于m、k的二元一次方程组.本题属于基础题,难度不大,解决该题型题目时,设出直角三角形一顶点的坐标,表示出其它两个顶点的坐标,再根据反比例函数图象上点的坐标特征找出方程组是关键.

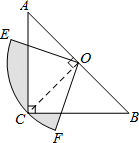 如图,在△ABC中,∠C=90°,AC=BC,斜边AB=4$\sqrt{2}$,O是AB的中点,以O为圆心,线段OC的长为半径画圆心角为90°的扇形OEF,$\widehat{EF}$经过点C,则图中阴影部分的面积为( )
如图,在△ABC中,∠C=90°,AC=BC,斜边AB=4$\sqrt{2}$,O是AB的中点,以O为圆心,线段OC的长为半径画圆心角为90°的扇形OEF,$\widehat{EF}$经过点C,则图中阴影部分的面积为( )| A. | 2π-4 | B. | 4-π | C. | π-2 | D. | 4π-8 |
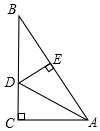 如图,在Rt△ABC中,∠C=90°,AD平分∠CAB,点D到AB的距离DE=1cm,BE=$\sqrt{3}$cm,则BC等于( )
如图,在Rt△ABC中,∠C=90°,AD平分∠CAB,点D到AB的距离DE=1cm,BE=$\sqrt{3}$cm,则BC等于( )| A. | 1cm | B. | 2cm | C. | 3cm | D. | ($\sqrt{3}$+1)cm |
| 薄板的边长x(cm) | 20 | 30 |
| 出厂价y(元/张) | 50 | 70 |
(2)每张薄板的成本价w(单位:元)与它的面积x2(单位:cm2)成正比例,已知出厂一张边长为40cm的薄板,获得利润p是26元(利润=出厂价-成本价),
①求一张薄板的利润p与边长x之间满足的函数关系式.
②当边长为多少时,出厂一张薄板所获得的利润最大?最大利润是多少?