题目内容
3. 如图,PA、PB分别切⊙O于点A、B,点E是⊙O上一点,且∠AEB=50°,则∠P=( )
如图,PA、PB分别切⊙O于点A、B,点E是⊙O上一点,且∠AEB=50°,则∠P=( )| A. | 100° | B. | 80° | C. | 60° | D. | 50° |
分析 连接OA,BO,由圆周角定理知可知∠AOB=2∠AEB=100°,PA、PB分别切⊙O于点A、B,利用切线的性质可知∠OAP=∠OBP=90°,根据四边形内角和可求得∠P的度数.
解答 解:连接OA,BO; ∵∠AOB=2∠E=100°,
∵∠AOB=2∠E=100°,
∵PA、PB分别切⊙O于点A、B,
∴∠OAP=∠OBP=90°,
∴∠P=180°-∠AOB=80°,
故选B.
点评 本题考查了切线的性质,利用了圆周角定理,切线的性质,四边形的内角和为360度求解,连接OA,OB构造垂直是解题关键.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目
11.下列实数中,是无理数的为( )
| A. | 0.3 | B. | 0 | C. | $\sqrt{3}$ | D. | $\frac{1}{3}$ |
12.将抛物线y=-2x2向上平移3个单位,再向左平移2个单位,那么得到的抛物线的解析式为( )
| A. | y=-2(x+2)2+3 | B. | y=-2(x+3)2-2 | C. | y=-2(x-2)2+3 | D. | y=-2(x+3)2+2 |
13.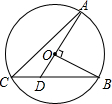 如图,OA,OB是⊙O的半径,且OA⊥OB,AO的延长线与弦BC交于点D,连结AC.若∠B=25°,则∠A的度数是( )
如图,OA,OB是⊙O的半径,且OA⊥OB,AO的延长线与弦BC交于点D,连结AC.若∠B=25°,则∠A的度数是( )
 如图,OA,OB是⊙O的半径,且OA⊥OB,AO的延长线与弦BC交于点D,连结AC.若∠B=25°,则∠A的度数是( )
如图,OA,OB是⊙O的半径,且OA⊥OB,AO的延长线与弦BC交于点D,连结AC.若∠B=25°,则∠A的度数是( )| A. | 65° | B. | 45° | C. | 25° | D. | 20° |
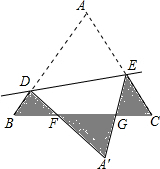 如图,等边△ABC的面积为为$\sqrt{3}$cm2,D、E分别是AB、AC上的点,将△ABC沿直线DE折叠,点A落在A′处,且A′在△ABC外部,则阴影部分图象的周长为6cm.
如图,等边△ABC的面积为为$\sqrt{3}$cm2,D、E分别是AB、AC上的点,将△ABC沿直线DE折叠,点A落在A′处,且A′在△ABC外部,则阴影部分图象的周长为6cm. 如图,AB为⊙O的直径,BC切⊙O于点B,AC交⊙O于点D,E为BC中点.求证:DE为⊙O的切线.
如图,AB为⊙O的直径,BC切⊙O于点B,AC交⊙O于点D,E为BC中点.求证:DE为⊙O的切线.