题目内容
4.已知二次函数y=2x2+8x+m,自变量x1=-2+$\sqrt{3}$对应的函数值为y1,自变量x2=-4对应的函数值为y2,则y1<y2(填“>”、“<”或“﹦”).分析 先根据二次函数的性质求出抛物线的对称轴为直线x=-2,然后通过比较点(-2+$\sqrt{3}$,y1)和点(-4,y2)离直线x=-2的远近得到y1与y2的大小.
解答 解:∴抛物线的对称轴为直线x=-$\frac{8}{2×2}$=-2,
∴点(-2+$\sqrt{3}$,y1)比点(-4,y2)离直线x=-2要近,
而抛物线开口向上,
∴y1<y2.
故答案为<.
点评 本题考查了二次函数图象上点的坐标特征,本题的关键是(1)找到二次函数的对称轴;(2)掌握二次函数y=ax2+bx+c(a≠0)的图象性质.

练习册系列答案
相关题目
12.将抛物线y=-2x2向上平移3个单位,再向左平移2个单位,那么得到的抛物线的解析式为( )
| A. | y=-2(x+2)2+3 | B. | y=-2(x+3)2-2 | C. | y=-2(x-2)2+3 | D. | y=-2(x+3)2+2 |
19.若分式$\frac{{x}^{2}-1}{x-1}$的值为0,则应满足的条件是( )
| A. | x≠1 | B. | x=-1 | C. | x=1 | D. | x=±1 |
9.抛物线y=(x+1)(x-3)的对称轴是直线( )
| A. | x=-1 | B. | x=1 | C. | x=-3 | D. | x=3 |
13.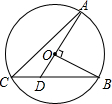 如图,OA,OB是⊙O的半径,且OA⊥OB,AO的延长线与弦BC交于点D,连结AC.若∠B=25°,则∠A的度数是( )
如图,OA,OB是⊙O的半径,且OA⊥OB,AO的延长线与弦BC交于点D,连结AC.若∠B=25°,则∠A的度数是( )
 如图,OA,OB是⊙O的半径,且OA⊥OB,AO的延长线与弦BC交于点D,连结AC.若∠B=25°,则∠A的度数是( )
如图,OA,OB是⊙O的半径,且OA⊥OB,AO的延长线与弦BC交于点D,连结AC.若∠B=25°,则∠A的度数是( )| A. | 65° | B. | 45° | C. | 25° | D. | 20° |
14.若一个多边形的内角和是其外角和的4倍,则此多边形的对角线共有( )
| A. | 35条 | B. | 40条 | C. | 10条 | D. | 50条 |
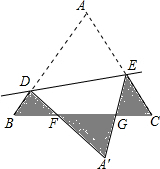 如图,等边△ABC的面积为为$\sqrt{3}$cm2,D、E分别是AB、AC上的点,将△ABC沿直线DE折叠,点A落在A′处,且A′在△ABC外部,则阴影部分图象的周长为6cm.
如图,等边△ABC的面积为为$\sqrt{3}$cm2,D、E分别是AB、AC上的点,将△ABC沿直线DE折叠,点A落在A′处,且A′在△ABC外部,则阴影部分图象的周长为6cm.