题目内容
17.一次安全知识测验中,学生得分均为整数,满分10分,这次测验中甲、乙两组学生人数都为6人,成绩如下(单位:分):甲:7,9,10,8,5,9;
乙:9,6,8,10,7,8
(1)请补充完整下面的成绩统计分析表:
| 平均分 | 方差 | 众数 | 中位数 | |
| 甲组 | 8 | $\frac{8}{3}$ | 9 | 8.5 |
| 乙组 | 8 | $\frac{5}{3}$ | 8 | 8 |
分析 (1)利用平均数、方差的计算公式即可求得乙组平均数与甲组方差,然后根据中位数的定义,求出甲组中位数即可求出答案;
(2)根据已知条件以及(1)中表格所求数据,可知两组平均分相同,但乙组的方差小于甲组的方差,所以乙的成绩更稳定,乙组的成绩要好于甲组.
解答 解:(1)乙组平均数为:(9+6+8+10+7+8)÷6=8;
甲组方差为:$\frac{1}{6}$[(7-8)2+(9-8)2+(10-8)2+(8-8)2+(5-8)2+(9-8)2]=$\frac{8}{3}$,
甲组成绩按从小到大的顺序排列为5,7,8,9,9,10,第三个与第四个数据分别是8,9,所以中位数是:(8+9)÷2=8.5.
填表如下:
| 平均分 | 方差 | 众数 | 中位数 | |
| 甲组 | 8 | $\frac{8}{3}$ | 9 | 8.5 |
| 乙组 | 8 | $\frac{5}{3}$ | 8 | 8 |
故答案为$\frac{8}{3}$,8.5,8;两队平均分相同,但乙的方差小于甲的方差,所以乙的成绩更稳定.
点评 本题考查方差的定义与意义:一般地设n个数据,x1,x2,…xn的平均数为$\overline{x}$,则方差S2=$\frac{1}{n}$[(x1-$\overline{x}$)2+(x2-$\overline{x}$)2+…+(xn-$\overline{x}$)2],它反映了一组数据的波动大小,方差越大,波动性越大,反之也成立.也考查了平均数、众数与中位数.

练习册系列答案
相关题目
8.使分式$\frac{x}{x+2}$有意义的x的取值范围是( )
| A. | x≠-2 | B. | x≠0 | C. | x>-2 | D. | x<-2 |
2.如果分式$\frac{x-2}{x+3}$的值为零,那么x的值是( )
| A. | x=2 | B. | x=-3 | C. | x=-2 | D. | x=3 |
9.我们用有理数的运算研究下面问题.规定:水位上升为正,水位下降为负;几天后为正,几天前为负.如果水位每天下降4cm,那么3天后的水位变化用算式表示正确的是( )
| A. | (+4)×(+3) | B. | (+4)×(-3) | C. | (-4)×(+3) | D. | (-4)×(-3) |
 如图,DE⊥EB于点E,∠1=∠C,∠2与∠C互为余角,判断DE与BC是否平行,并说明理由.
如图,DE⊥EB于点E,∠1=∠C,∠2与∠C互为余角,判断DE与BC是否平行,并说明理由.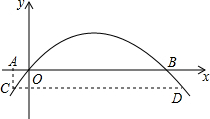 如图是某拱形大桥的示意图,桥拱与桥面的交点为O,B,以点O为原点,水平直线OB为x轴,建立平面直角坐标系,桥的拱形可以近似看成抛物线y=-$\frac{1}{400}$(x-80)2+16,桥拱与桥墩AC的交点C恰好在水面,有AC⊥x轴.若OA=10米,则桥面离水面的高度AC为$\frac{17}{4}$米.
如图是某拱形大桥的示意图,桥拱与桥面的交点为O,B,以点O为原点,水平直线OB为x轴,建立平面直角坐标系,桥的拱形可以近似看成抛物线y=-$\frac{1}{400}$(x-80)2+16,桥拱与桥墩AC的交点C恰好在水面,有AC⊥x轴.若OA=10米,则桥面离水面的高度AC为$\frac{17}{4}$米.