题目内容
3. 在△ABC中,∠A=60°,∠ABC,∠ACB所对的边b,c满足b2+c2-4(b+c)+8=0.
在△ABC中,∠A=60°,∠ABC,∠ACB所对的边b,c满足b2+c2-4(b+c)+8=0.(1)证明:△ABC是边长为2的等边三角形.
(2)若b,c两边上的中线BD,CE交于点O,求OD:OB的值.
分析 (1)由b2+c2-2(b+c)+2=0,可以判定b=c,∠A=60°可以确定△ABC是边长为1的等边三角形;
(2)连接DE,点D、E分别是边AC、AB边上的中点,所以DE∥BC,DE=$\frac{1}{2}$BC,∴△DEO∽△BOC,即可得到答案.
解答 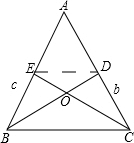 解:(1)∵b2+c2-4(b+c)+8=0,
解:(1)∵b2+c2-4(b+c)+8=0,
∴(b-2)2+(c-2)2=0,
∴b=c=2,
又∵∠A=60°,
所以△ABC是边长为2的等边三角形;
(2)连接DE,
∵点D、E分别是边AC、AB边上的中点,
所以DE∥BC,DE=$\frac{1}{2}$BC,
∵DE∥BC,
∴△DEO∽△BOC,
∴$\frac{DE}{BC}$=$\frac{OD}{OB}$=$\frac{1}{2}$
点评 本题考查因式分解的应用以及相似三角形的综合应用,解答本题的关在在于熟记公式的转化和相似三角形的判定方法和性质的综合应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.三角形的一个外角等于与它不相邻的一个内角的4倍,等于与它相邻的内角的2倍,则该三角形各角的度数为( )
| A. | 45、45、90 | B. | 30、60、90 | C. | 25、25、130 | D. | 36、72、72 |
18.已知P1(-2,y1),P2(3,y2)是一次函数y=-x+b(b为常数)的图象上的两个点,则y1,y2的大小关系是( )
| A. | y1<y2 | B. | y1>y2 | C. | y1=y2 | D. | 不能确定 |
8.使分式$\frac{x}{x+2}$有意义的x的取值范围是( )
| A. | x≠-2 | B. | x≠0 | C. | x>-2 | D. | x<-2 |
 如图,△ABC中,D,E分别在边AB,AC上,DE∥BC,若∠A=60°,∠B=70°,则∠AED的度数为50°.
如图,△ABC中,D,E分别在边AB,AC上,DE∥BC,若∠A=60°,∠B=70°,则∠AED的度数为50°.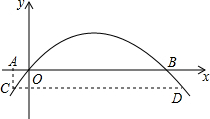 如图是某拱形大桥的示意图,桥拱与桥面的交点为O,B,以点O为原点,水平直线OB为x轴,建立平面直角坐标系,桥的拱形可以近似看成抛物线y=-$\frac{1}{400}$(x-80)2+16,桥拱与桥墩AC的交点C恰好在水面,有AC⊥x轴.若OA=10米,则桥面离水面的高度AC为$\frac{17}{4}$米.
如图是某拱形大桥的示意图,桥拱与桥面的交点为O,B,以点O为原点,水平直线OB为x轴,建立平面直角坐标系,桥的拱形可以近似看成抛物线y=-$\frac{1}{400}$(x-80)2+16,桥拱与桥墩AC的交点C恰好在水面,有AC⊥x轴.若OA=10米,则桥面离水面的高度AC为$\frac{17}{4}$米.