题目内容
18. 如图,?OABC的顶点C在x轴的正半轴上,顶点A、B在第一象限内,且点A的横坐标为2,对角线AC与OB交于点D.反比例函数$y=\frac{k}{x}$的图象经过点A与点D,若?OABC的面积为24,则k的值为( )
如图,?OABC的顶点C在x轴的正半轴上,顶点A、B在第一象限内,且点A的横坐标为2,对角线AC与OB交于点D.反比例函数$y=\frac{k}{x}$的图象经过点A与点D,若?OABC的面积为24,则k的值为( )| A. | .12 | B. | .10 | C. | .8 | D. | .6 |
分析 分别过A、D两点作x轴的垂线,交x轴于点E、F,则可用k表示出AE,利用平行四边形的性质可表示出DF,则可求得D点横坐标,且可求得AE=EF=CF=2,从而可表示出四边形OABC的面积,可求得k.
解答 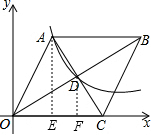 解:
解:
如图,分别过A、D两点作x轴的垂线,交x轴于点E、F,
∵$y=\frac{k}{x}$的图象经过点A,且A点横坐标为2,
∴AE=$\frac{k}{2}$,
∵四边形OABC为平行四边形,
∴D为AC中点,且DF∥AE,
∴DF=$\frac{1}{2}$AE=$\frac{k}{4}$,且EF=FC,
∵D点在反比例函数图象上,
∴D点横坐标为4,
∴EF=OF-OE=4-2=2,
∴OC=OF+FC=OF+EF=4+2=6,
∴S△OCD=$\frac{1}{2}$OC•DF=$\frac{1}{2}$×6×$\frac{k}{4}$=$\frac{3k}{4}$,
∵四边形OABC为平行四边形,
∴S四边形OABC=4S△OCD,
∴4×$\frac{3k}{4}$=24,解得k=8,
故选C.
点评 本题考查了平行四边形的性质及反比例函数k的几何意义,涉及的知识点较多,注意理清解题思路,分步求解.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
8.4的平方根是( )
| A. | ±2 | B. | $\frac{1}{2}$ | C. | 2 | D. | -2 |
9.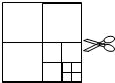 如图,将一张正方形纸片剪成四个小正方形,得到4个小正方形,称为第一次操作;然后,将其中的一个正方形再剪成四个小正方形,共得到7个小正方形,称为第二次操作;再将其中的一个正方形再剪成四个小正方形,共得到10个小正方形,称为第三次操作;…,根据以上操作,若要得到2017个小正方形,则需要操作的次数是( )
如图,将一张正方形纸片剪成四个小正方形,得到4个小正方形,称为第一次操作;然后,将其中的一个正方形再剪成四个小正方形,共得到7个小正方形,称为第二次操作;再将其中的一个正方形再剪成四个小正方形,共得到10个小正方形,称为第三次操作;…,根据以上操作,若要得到2017个小正方形,则需要操作的次数是( )
 如图,将一张正方形纸片剪成四个小正方形,得到4个小正方形,称为第一次操作;然后,将其中的一个正方形再剪成四个小正方形,共得到7个小正方形,称为第二次操作;再将其中的一个正方形再剪成四个小正方形,共得到10个小正方形,称为第三次操作;…,根据以上操作,若要得到2017个小正方形,则需要操作的次数是( )
如图,将一张正方形纸片剪成四个小正方形,得到4个小正方形,称为第一次操作;然后,将其中的一个正方形再剪成四个小正方形,共得到7个小正方形,称为第二次操作;再将其中的一个正方形再剪成四个小正方形,共得到10个小正方形,称为第三次操作;…,根据以上操作,若要得到2017个小正方形,则需要操作的次数是( )| A. | 672 | B. | 671 | C. | 670 | D. | 674 |
6.下列二次根式中,是最简二次根式的是( )
| A. | 2$\sqrt{3}$ | B. | $\sqrt{12}$ | C. | $\sqrt{\frac{1}{2}}$ | D. | $\sqrt{{x}^{4}+{x}^{3}{y}^{2}}$ |
13.已知正比例函数y=kx(k≠0)的图象经过点(1,3),则k的值为( )
| A. | 3 | B. | -3 | C. | $\frac{1}{3}$ | D. | $-\frac{1}{3}$ |
3.等腰三角形周长为13cm,其中一边长为3cm,则该等腰三角形的底边长为( )
| A. | 7 cm | B. | 3 cm | C. | 7 cm或3 cm | D. | 8 cm |
10.下列运算中,正确的是( )
| A. | x3÷x=x4 | B. | a2+a2=2a4 | C. | 3x-2x=1 | D. | 3x-2x=x |
7.下列命题为真命题的是( )
| A. | 若a2=b2,则a=b | |
| B. | 等角的补角相等 | |
| C. | n边形的外角和为(n-2)•180° | |
| D. | 若x甲=x乙,S2甲>S2乙,则甲数据更稳定 |