Question

15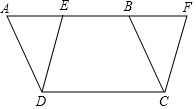．如图，在平行四边形ABCD中，点E是AB边上任意一点，连接DE．过点C作线段DE的平行线，交AB延长线于点F．
（1）证明：AE=BF．
（2）过点E作EG⊥CF，垂足为点G．点M为DC边中点，连接ME，MG．
①根据题意完成作图；
②猜想线段ME，MG的数量关系，并写出你的证明思路．

Answer 1

分析 （1）只要证明四边形EFCD是平行四边形，可得EF=CD=AB，即可推出AE=BF；
（2））①作图，如图所示；
②猜想：ME=MG，只要证明△DEM≌△CHM，可得EM=MH，再根据直角三角形斜边中线定理即可证明；

解答 （1）证明：∵四边形ABCD是平行四边形，
∴AB=CD，AB∥CD，
又∵DE∥CF，
∴四边形DEFC是平行四边形，
∴EF=CD，
∴EF=AB，
∴EF-BE=AB-BE，
∴AE=BF．

（2）①作图，如图所示．

②猜想：ME=MG．
理由：延长EM，FC交于点．
∵DE∥FH，
∴∠DEM=∠H，
在△DEM和△CHM中，
$\left\{\begin{array}{l}{∠DEM=∠H}\\{∠DME=∠HMC}\\{DM=MC}\end{array}\right.$，
∴△DEM≌△CHM，
∴ME=MH，
∵EG⊥FH，
在Rt△EHG中，∵EM=MH，
∴GM=EM=MH，
∴ME=MG．

点评 本题考查复杂作图，全等三角形的判定和性质、平行四边形的性质和判定等知识，解题的关键是学会添加常用辅助线，构造全等三角形解决问题．