题目内容
8.在平面直角坐标系中,四边形ABCD的三个顶点的坐标分别为A(-1,0),B(-1,-2),C(3,-6),已知AB∥CD,点D在x轴上,线段BC交y轴于点E.(1)请直接写出点D的坐标为(3,0);
(2)求出点D到点B之间的距离;
(3)试分别求出△ABE和四边形ABCD的面积.
分析 (1)根据平行线的性质,可得答案;
(2)根据勾股定理,可得答案;
(3)根据平行间的距离相等,可得三角形的高OA,根据三角形的面积公式,可得答案;
根据梯形的面积公式,可得答案.
解答 解:如图: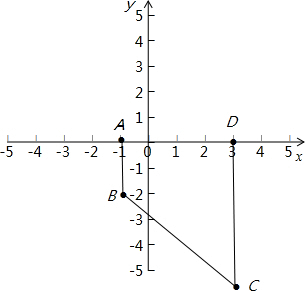
(1)CD∥AB,(3,-6),
请直接写出点D的坐标为(3,0),
故答案为:(3,0);
(2)在RtABD中,AB=|-2|=2,AD=3-(-1)=4,
由勾股定理,得
BD=$\sqrt{A{B}^{2}+A{D}^{2}}$=$\sqrt{{2}^{2}+{4}^{2}}$=2$\sqrt{5}$,
点D到点B之间的距离是2$\sqrt{5}$;
(3)由A(-1,0),B(-1,-2),得
OA=1,AB=2.S△ABE=$\frac{1}{2}$AB•OA=$\frac{1}{2}$×2×1=1,
由A(-1,0),B(-1,-2),C(3,-6),D(3,0),
得AB=2,CD=6,AD=4.
S四边形ABCD=$\frac{1}{2}$(AB+CD)•AD
=$\frac{1}{2}$×(2+6)×4=16,
答:△ABE的面积是1,四边形ABCD的面积16.
点评 本题考查了坐标与图形的性质,横坐标相等点在平行y轴的直线上,平行同一条直线的两条直线互相平行,注意△ABE的底是AB,高是OA.

练习册系列答案
相关题目
 已知线段AB上顺次有三个点C、D、E,把线段AB分成2:3:4:5四部分,且AB=56cm.
已知线段AB上顺次有三个点C、D、E,把线段AB分成2:3:4:5四部分,且AB=56cm.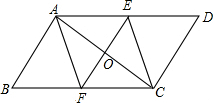 如图,E、F分别是?ABCD的边AD、BC的中点,EF和AC相交于O,则AC、EF互相平分,说明你的理由.
如图,E、F分别是?ABCD的边AD、BC的中点,EF和AC相交于O,则AC、EF互相平分,说明你的理由.