题目内容
19．方程x2+2kx+k2-2k+1=0的两个实数根x1，x2满足x12+x22=4，求k的值．分析 由x12+x22=x12+2x1•x2+x22-2x1•x2=（x1+x2）2-2x1•x2=4，然后根据根与系数的关系即可得到一个关于k的方程，从而求得k的值．
解答 解：∵方程x2+2kx+k2-2k+1=0的两个实数根，
∴△=4k2-4（k2-2k+1）≥0，
解得 k≥$\frac{1}{2}$．
∵x12+x22=4，
∴x12+x22=x12+2x1•x2+x22-2x1•x2=（x1+x2）2-2x1•x2=4，
又∵x1+x2=-2k，x1•x2=k2-2k+1，
代入上式有4k2-2（k2-2k+1）=4，
解得k=1或k=-3（不合题意，舍去）．
∴k=1．
点评 本题考查了根与系数的关系的知识，解答本题要掌握若x1，x2是一元二次方程ax2+bx+c=0（a≠0）的两根时，x1+x2=-$\frac{b}{a}$，x1x2=$\frac{c}{a}$．
练习册系列答案
相关题目
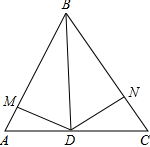如图，在△ABC中，BD平分∠ABC，M、N分别是BA、BC上的点，且∠MDN+∠MBN=180°，求证：DM=DN．
在图中作出△ABC关于x轴的对称图形△A1B1C1．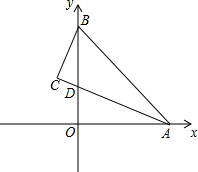
如图，在平面直角坐标系中，点A在x轴上，点B、D在y轴上，OA=OB，点D的坐标为（0，4），过点B作BC⊥AD，交AD的延长线于点C，且2BC=AD．
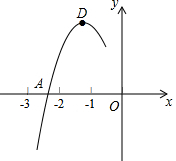抛物线y=ax2+bx+c的顶点为D（-1，2），与x轴的一个交点A在点（-3，0）和（-2，0）之间，其部分图象如图，则以下结论：