题目内容
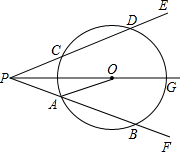 如图,射线PG平分∠EPF,O为射线PG上一点,以O为圆心、10为半径作⊙O,分别与∠EPF的两边相交于A,B和C,D,连接OA,此时有OA∥PE,若弦AB=12,求OP的长.
如图,射线PG平分∠EPF,O为射线PG上一点,以O为圆心、10为半径作⊙O,分别与∠EPF的两边相交于A,B和C,D,连接OA,此时有OA∥PE,若弦AB=12,求OP的长.考点:垂径定理,角平分线的性质,勾股定理
专题:计算题
分析:作OH⊥AB于H,如图根据垂径定理得AH=
AB=6,在Rt△AOH中利用勾股定理计算出OH=8,再由PG平分∠EPF得到∠EPO=∠FPO,由OA∥PE得∠EPO=∠POA,则∠POA=∠OPA,根据等腰三角形的判定得AP=AO=10,则PH=PA+AH=16,然后在Rt△POH中根据勾股定理计算OP.
| 1 |
| 2 |
解答:解:作OH⊥AB于H,如图,
则AH=BH=
AB=6,
在Rt△AOH中,∵OA=10,AH=6,
∴OH=
=8,
∵PG平分∠EPF,
∴∠EPO=∠FPO,
∵OA∥PE,
∴∠EPO=∠POA,
∴∠POA=∠OPA,
∴AP=AO=10,
∴PH=PA+AH=16,
在Rt△POH中,OP=
=8
.

则AH=BH=
| 1 |
| 2 |
在Rt△AOH中,∵OA=10,AH=6,
∴OH=
| OA2-AH2 |
∵PG平分∠EPF,
∴∠EPO=∠FPO,
∵OA∥PE,
∴∠EPO=∠POA,
∴∠POA=∠OPA,
∴AP=AO=10,
∴PH=PA+AH=16,
在Rt△POH中,OP=
| PH2+OH2 |
| 5 |
点评:本题考查了垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的两条弧.同时利用角平分线的性质和勾股定理.作弦的垂线是常用的辅助线.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
下列各数中是无理数的是( )
| A、1.232232223 | |||
B、
| |||
C、
| |||
D、
|
下列是计算正确的是( )
| A、-8-3=-5 |
| B、-(-2)2=4 |
| C、-(x-y)=x+y |
| D、ab+2ba=3ab |