题目内容
 在四边形ABCD中,对角线AC与BD交于点O,△ABO≌△CDO.
在四边形ABCD中,对角线AC与BD交于点O,△ABO≌△CDO.(1)求证:四边形ABCD为平行四边形;
(2)若∠DAO=∠CBO,求证:四边形ABCD为矩形.
考点:矩形的判定,平行四边形的判定
专题:证明题
分析:(1)根据全等三角形的对应边相等可得AO=CO,BO=DO,再根据对角线互相平分的四边形是平行四边形证明;
(2)根据平行线的性质得出内错角相等,再根据等角对等边的性质可得BO=CO,从而得到AC=BD,然后根据对角线相等的平行四边形是矩形证明.
(2)根据平行线的性质得出内错角相等,再根据等角对等边的性质可得BO=CO,从而得到AC=BD,然后根据对角线相等的平行四边形是矩形证明.
解答:(1)证明:∵△ABO≌△CDO,
∴AO=CO,BO=DO,
∴AC、BD互相平分,
∴四边形ABCD是平行四边形;

(2)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠DAO=∠BCA,
∵∠DAO=∠CBO,
∴∠ABO=∠BAO,
∴∠CBO=∠BAO,
∴CO=BO,
又∵AO=CO,BO=DO,
∴AC=BD,
∴?ABCD是矩形(对角线相等的平行四边形是矩形).
∴AO=CO,BO=DO,
∴AC、BD互相平分,
∴四边形ABCD是平行四边形;

(2)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠DAO=∠BCA,
∵∠DAO=∠CBO,
∴∠ABO=∠BAO,
∴∠CBO=∠BAO,
∴CO=BO,
又∵AO=CO,BO=DO,
∴AC=BD,
∴?ABCD是矩形(对角线相等的平行四边形是矩形).
点评:本题考查了矩形的判定,全等三角形的性质,平行四边形的判定与性质,注意全等三角形对应顶点的字母放在对应位置上是准确找出对应角与对应边的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知⊙O1的半径为1,⊙O2的半径为5,若⊙O1和⊙O2有2个公共点,则圆心距O1O2的长度可以是( )
| A、4 | B、5 | C、6 | D、9 |
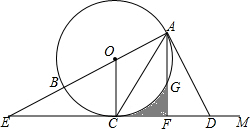 如图,AB是⊙O的直径,CM是⊙O的切线,切点为C,延长AB交CD于点E,连接AC,在射线CM上取一点D使DA=DC,作AF⊥ED于点F,交⊙O于点G,
如图,AB是⊙O的直径,CM是⊙O的切线,切点为C,延长AB交CD于点E,连接AC,在射线CM上取一点D使DA=DC,作AF⊥ED于点F,交⊙O于点G,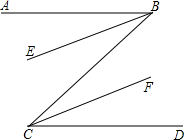 如图,已知:AB∥CD,甲、乙两人分别沿着BC与AB、CD的夹角的平分线运动,小明认为甲、乙两人运动的路线BE、CF平行.你认为正确吗?请说明理由.
如图,已知:AB∥CD,甲、乙两人分别沿着BC与AB、CD的夹角的平分线运动,小明认为甲、乙两人运动的路线BE、CF平行.你认为正确吗?请说明理由.