题目内容
11. 如图,已知⊙O是△ABC的外接圆,AB为直径,若PA⊥AB,PO过AC的中点M,求证:PC是⊙O的切线.
如图,已知⊙O是△ABC的外接圆,AB为直径,若PA⊥AB,PO过AC的中点M,求证:PC是⊙O的切线.
分析 连接OC,如图,先利用垂径定理的推理得到OM⊥AC,则可判断PO垂直平分AC,所以PA=PC,根据等腰三角形的性质得∠PAC=∠PCA,加上∠OAC=∠OCA,易得∠PCO=∠PA0=90°,然后根据切线的判定定理可得结论.
解答 证明:连接OC,如图,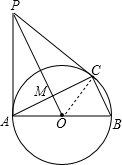
∵PA⊥AB,
∴∠PA0=900,
∵PO过AC的中点M,
∴OM⊥AC,
∴PO垂直平分AC,
∴PA=PC,
∴∠PAC=∠PCA,
而OA=OC,
∴∠OAC=∠OCA,
∴∠PCO=∠PCA+∠ACO=∠PAC+∠CAO=∠PA0=90°,
∴OC⊥PC,
∴PC是⊙O的切线.
点评 本题考查了切线的判定:经过半径的外端且垂直于这条半径的直线是圆的切线.当条件中明确指出直线与圆有公共点时,常连接过该公共点的半径,证明该半径垂直于这条直线,可简单地说成“有交点,作半径,证垂直”.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
16.△ABC中,∠C=90°,AC=12cm,BC=5cm,若以C为圆心,5cm为半径作圆,则斜边AB与⊙O的位置关系是( )
| A. | 相离 | B. | 相切 | C. | 相交 | D. | 不能确定 |




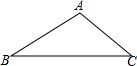 已知△ABC(如图),求作△A′B′C′,使A′B′=AB,A′C′=AC,∠B′=∠B,根据作图回答下列问题:
已知△ABC(如图),求作△A′B′C′,使A′B′=AB,A′C′=AC,∠B′=∠B,根据作图回答下列问题: