题目内容
20．
如图，四边形ABCD中，E、F、G、H依次是各边的中点，O是形内一点，若四边形AEOH、四边形BFOE、四边形CGOF的面积分别为5、6、7，试求四边形DHOG的面积．
分析 连接OC，OB，OA，OD，易证S△OBF=S△OCF，S△ODG=S△OCG，S△ODH=S△OAH，S△OAE=S△OBE，所以S四边形AEOH+S四边形CGOF=S四边形DHOG+S四边形BFOE，所以可以求出S四边形DHOG．
解答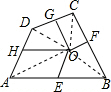 
解：连接OC，OB，OA，OD，
∵E、F、G、H依次是各边中点，
∴△AOE和△BOE等底等高，
∴S△OAE=S△OBE，
同理可证，S△OBF=S△OCF，S△ODG=S△OCG，S△ODH=S△OAH，
∴S四边形AEOH+S四边形CGOF=S四边形DHOG+S四边形BFOE，
∵S四边形AEOH=5，S四边形BFOE=6，S四边形CGOF=7，
∴5+7=6+S四边形DHOG，
解得：S四边形DHOG=6．
点评 本题考查了中点四边形、三角形的面积．解决本题的关键将各个四边形划分，充分利用给出的中点这个条件，证得三角形的面积相等，进而证得结论．
练习册系列答案
全优点练单元计划系列答案
相关题目
如图，△ABC中D、E、F分别是各边的中点，连接AE、DF．
15．若m为有理数，且|-m|=-m．那么m是（ ）
| A． | 非正数 | B． | 非负数 | C． | 负数 | D． | 不为零的数 |