题目内容
10.化简计算:$\sqrt{8}+2\sqrt{\frac{1}{3}}-(\sqrt{27}-\sqrt{2})$.分析 先把二次根式化为最简二次根式,再进行二次根式的加减,即可解答.
解答 解:$\sqrt{8}+2\sqrt{\frac{1}{3}}-(\sqrt{27}-\sqrt{2})$
=$2\sqrt{2}+\frac{2\sqrt{3}}{3}-3\sqrt{3}+\sqrt{2}$
=3$\sqrt{2}-\frac{7\sqrt{3}}{3}$.
点评 本题考查了二次根式的加减法,解决本题的关键是先把二次根式化为最简二次根式.

练习册系列答案
相关题目
1.若k>0,点P(-k,k)在第( )象限.
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
2. 如图,在同一平面内,两条平行的高速l1和l2间有一条“z”型道路连通,其中AB段与高速公路l1成30°角,CD与l2成40°的角,∠ABC=90°,则∠BCD的度数为( )
如图,在同一平面内,两条平行的高速l1和l2间有一条“z”型道路连通,其中AB段与高速公路l1成30°角,CD与l2成40°的角,∠ABC=90°,则∠BCD的度数为( )
 如图,在同一平面内,两条平行的高速l1和l2间有一条“z”型道路连通,其中AB段与高速公路l1成30°角,CD与l2成40°的角,∠ABC=90°,则∠BCD的度数为( )
如图,在同一平面内,两条平行的高速l1和l2间有一条“z”型道路连通,其中AB段与高速公路l1成30°角,CD与l2成40°的角,∠ABC=90°,则∠BCD的度数为( )| A. | 70° | B. | 90° | C. | 100° | D. | 110° |
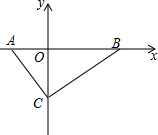 如图,在平面直角坐标系中,Rt△ABC的斜边AB在x轴上,AB=25,顶点C在y轴的负半轴上,tan∠ACO=$\frac{3}{4}$,点P在线段OC上,且PO、PC的长(PO<PC)是关于x的方程x2-12x+32=O的两根.
如图,在平面直角坐标系中,Rt△ABC的斜边AB在x轴上,AB=25,顶点C在y轴的负半轴上,tan∠ACO=$\frac{3}{4}$,点P在线段OC上,且PO、PC的长(PO<PC)是关于x的方程x2-12x+32=O的两根. 如图,AD∥BC,∠α=50°,∠B=∠C,请求出∠B,∠C,∠D的度数.
如图,AD∥BC,∠α=50°,∠B=∠C,请求出∠B,∠C,∠D的度数.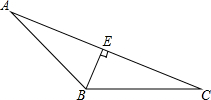 如图,在△ABC中,BE⊥AC,BC=5cm,AC=8cm,BE=3cm,
如图,在△ABC中,BE⊥AC,BC=5cm,AC=8cm,BE=3cm,