题目内容
已知：如图，△ABC中，DE∥BC，BE与CD交于点O，AO与DE，BC分别交于点N，M．（1）已知点M是BC的中点．求证：DN=EN；
（2）已知ON：OM=2：5，四边形BCED的面积为42，求△ABC的面积．
考点：相似三角形的判定与性质
专题：
分析：（1）由“平行线法”推知△ADN∽△ABM，则该相似三角形的对应边成比例：
=
．同理
=
，则
=
，根据“点M是BC的中点”易证DN=EN；
（2）通过证△EON∽△BOM，得到
=
=
=
．通过证△DOE∽△COB，得到
=
=
，故
=
，所以易求S△ABC=50．
| DN |
| BM |
| AN |
| AM |
| EN |
| CM |
| AN |
| AM |
| DN |
| BM |
| EN |
| CM |
（2）通过证△EON∽△BOM，得到
| EN |
| BM |
| OE |
| OB |
| ON |
| OM |
| 2 |
| 5 |
| OE |
| OB |
| DE |
| BC |
| 2 |
| 5 |
| S△ADE |
| S△ABC |
| 4 |
| 25 |
解答：（1）证明：如图，∵DE∥BC，
∴△ADN∽△ABM
∴
=
，
同理
=
，
∴
=
．
又∵点M是BC的中点，
∴BM=CM，
∴DN=EN；
（2）∵DE∥BC，
∴△EON∽△BOM，则
=
=
=
．
∵△DOE∽△COB，则
=
=
，
∴
=
，
∴设S△ADE=4x，则S△ABC=25x．
∵四边形BCED的面积为42，
∴25x-4x=42，
解得，x=2，
∴S△ABC=50．
∴△ADN∽△ABM
∴
| DN |
| BM |
| AN |
| AM |
同理
| EN |
| CM |
| AN |
| AM |
∴
| DN |
| BM |
| EN |
| CM |
又∵点M是BC的中点，
∴BM=CM，
∴DN=EN；
（2）∵DE∥BC，
∴△EON∽△BOM，则
| EN |
| BM |
| OE |
| OB |
| ON |
| OM |
| 2 |
| 5 |
∵△DOE∽△COB，则
| OE |
| OB |
| DE |
| BC |
| 2 |
| 5 |
∴
| S△ADE |
| S△ABC |
| 4 |
| 25 |
∴设S△ADE=4x，则S△ABC=25x．
∵四边形BCED的面积为42，
∴25x-4x=42，
解得，x=2，
∴S△ABC=50．
点评：本题考查了相似三角形的判定与性质．在判定两个三角形相似时，应注意利用图形中已有的公共角、公共边等隐含条件，以充分发挥基本图形的作用，寻找相似三角形的一般方法是通过作平行线构造相似三角形．
练习册系列答案
相关题目
如图，已知△ABC，过点A画一条平分三角形面积的直线．
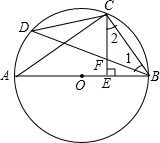如图，AB是⊙O的直径，C是