题目内容
18.化简:(1)$\frac{1}{{a}^{2}b}$-$\frac{b}{a{b}^{2}}$;
(2)$\frac{3x}{(x-3)^{2}}$-$\frac{x}{3-x}$;
(3)$\frac{1}{x-1}$+$\frac{1}{{x}^{2}-2x+1}$.
分析 (1)原式通分并利用同分母分式的减法法则计算,约分即可得到结果;
(2)原式通分并利用同分母分式的加法法则计算即可得到结果;
(3)原式通分并利用同分母分式的加法法则计算即可得到结果.
解答 解:(1)原式=$\frac{b}{{a}^{2}{b}^{2}}$-$\frac{ab}{{a}^{2}{b}^{2}}$=$\frac{b(1-a)}{{a}^{2}{b}^{2}}$=$\frac{1-a}{{a}^{2}b}$;
(2)原式=$\frac{3x}{(x-3)^{2}}$+$\frac{x}{x-3}$=$\frac{3x+x(x-3)}{(x-3)^{2}}$=$\frac{{x}^{2}}{(x-3)^{2}}$;
(3)原式=$\frac{x-1}{(x-1)^{2}}$+$\frac{1}{(x-1)^{2}}$=$\frac{x}{(x-1)^{2}}$.
点评 此题考查了分式的加减法,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
8.下列图形中,∠1和∠2不是同位角的是( )
| A. |  | B. |  | C. |  | D. |  |
20.《重庆市国民经济和社会发展第十二个五年规划纲要》提出:到2015年,逐步形成西部地区的重要增长极,地区生产总值达到15000亿元.将数据15000亿用科学记数法表示为( )亿.
| A. | 1.5×1011 | B. | 1.5×1012 | C. | 1.5×103 | D. | 1.5×104 |
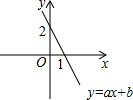 函数y=ax+b的图象如图所示,则不等式组$\left\{\begin{array}{l}{ax+b>0}\\{x+2>0}\end{array}\right.$的解集为-2<x<1.
函数y=ax+b的图象如图所示,则不等式组$\left\{\begin{array}{l}{ax+b>0}\\{x+2>0}\end{array}\right.$的解集为-2<x<1.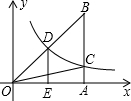 如图,已知反比例函数的图象经过直角△OAB斜边OB的中点D,与直角边AB相交于点C.若△OBC的面积为12,求这个反比例函数的解析式.
如图,已知反比例函数的图象经过直角△OAB斜边OB的中点D,与直角边AB相交于点C.若△OBC的面积为12,求这个反比例函数的解析式.