题目内容
4.已知二次函数y=-x2+2x-3,用配方法化为y=a(x-h)2+k的形式,结果是( )| A. | y=-(x-1)2-2 | B. | y=-(x-1)2+2 | C. | y=-(x-1)2+4 | D. | y=-(x+1)2-4 |
分析 利用配方法先提出二次项系数,再加上一次项系数的一半的平方来凑完全平方式,把一般式转化为顶点式.
解答 解:y=-x2+2x-3=-(x2-2x+1)+1-3=-(x-1)2-2,
故选A.
点评 本题考查了二次函数解析式的三种形式:
(1)一般式:y=ax2+bx+c(a≠0,a、b、c为常数);(2)顶点式:y=a(x-h)2+k;(3)交点式(与x轴):y=a(x-x1)(x-x2).

练习册系列答案
相关题目
19.将正偶数按表格方式排成5列若干行:
根据上述规律,数2016应在( )
| 第1列 | 第2列 | 第3列 | 第4列 | 第5列 | |
| 第1行 | 2 | 4 | 6 | 8 | |
| 第2行 | 16 | 14 | 12 | 10 | |
| 第3行 | 18 | 20 | 22 | 24 | |
| 第4行 | 32 | 30 | 28 | 26 | |
| … | … | … | … | … | … |
| A. | 第251行 第1列 | B. | 第251行 第5列 | C. | 第252行 第4列 | D. | 第252行 第1列 |
16.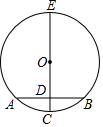 如图,CE是圆O的直径,⊙O的直径,AB为⊙O的弦,EC⊥AB,垂足为D,下面结论正确的有( )
如图,CE是圆O的直径,⊙O的直径,AB为⊙O的弦,EC⊥AB,垂足为D,下面结论正确的有( )
①AD=BD;②$\widehat{AC}$=$\widehat{BC}$;③$\widehat{AE}$=$\widehat{BE}$;④OD=CD.
 如图,CE是圆O的直径,⊙O的直径,AB为⊙O的弦,EC⊥AB,垂足为D,下面结论正确的有( )
如图,CE是圆O的直径,⊙O的直径,AB为⊙O的弦,EC⊥AB,垂足为D,下面结论正确的有( )①AD=BD;②$\widehat{AC}$=$\widehat{BC}$;③$\widehat{AE}$=$\widehat{BE}$;④OD=CD.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
14.若$\sqrt{m}$与$\sqrt{32}$是同类二次根式,则m的最小正整数值是( )
| A. | 16 | B. | 8 | C. | 4 | D. | 2 |
 如图是一个数值转换器,当输入-1时,请计算出输出结果?(要有计算过程)
如图是一个数值转换器,当输入-1时,请计算出输出结果?(要有计算过程)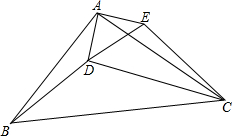 如图,△ABC中,AB=AC,点D在△ABC内部,以AD为腰作等腰△ADE,AD=AE,且∠BAC=∠DAE=100°,∠BDC=140°,∠BDA=α,连接BD、CD,当α=130°时,试判断△CDE的形状,并说明理由.
如图,△ABC中,AB=AC,点D在△ABC内部,以AD为腰作等腰△ADE,AD=AE,且∠BAC=∠DAE=100°,∠BDC=140°,∠BDA=α,连接BD、CD,当α=130°时,试判断△CDE的形状,并说明理由.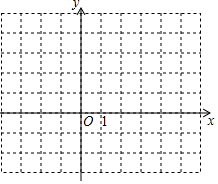 已知二次函数y=$\frac{1}{2}$x2-x-$\frac{3}{2}$.
已知二次函数y=$\frac{1}{2}$x2-x-$\frac{3}{2}$.