题目内容
1.(1)写一个多项式,再把它分解因式(要求:多项式含有字母m和n,系数、次数不限,并能先用提取公因式法再用公式法分解).(2)拆项法是因式分解中一种技巧性较强的方法,它通常是把多项式中的某一项拆成几项,再分组分解,因而有时需要多次实验才能成功,例如把 x3-3x2+4 分解因式,这是一个三项式,最高次项是三次项,一次项系数是0,本题没有公因式可提取,又不能直接应用公式,因而考虑制造分组分解的条件,把常数项拆成1和3,原式就变成
(x3+1)-(3x2-3),再利用立方和与平方差先分解,解法如下“
原式=x3+1-(3x2-3)=(x+1)(x2-x+1)-3(x+1)(x-1)=(x+1)(x2-x+1-3x+3)=(x+1)(x-2)2
公式:a3+b3=(a+b)(a2-ab+b2) a3-b3=(a-b)(a2+ab+b2)
根据上述论法和解法,
(1)分解因式 x3+x2-2
(2)分解因式 x3-7x+6
(3)分解因式 x4+x2+1.
分析 (1)将原式拆成(x3-1)+(x2-1)然后分别利用立方差和平方差公式因式分解后再提起公因式x-1即可;
(2)将原式拆成x3-1-7x+7,然后前两项利用立方差公式因式分解,后两项提取公因式即可确定答案;
(3)将原式拆成x4+2x2+1-x2,然后利用平方差公式因式分解即可.
解答 解:(1)x3+x2-2
=(x3-1)+(x2-1)
=(x-1)(x2+x+1)+(x-1)(x+1)
=(x-1)(x2+2x+2);
(2)原式=x3-1-7x+7=(x-1)(x2+x+1)-7(x-1)=(x-1)(x2+x-6)=(x-1)(x-2)(x+3);
(3)x4+x2+1=x4+2x2+1-x2=(x2+1)2-x2=(x2+1+x)(x2+1-x).
点评 本题考查了因式分解的应用,解题的关键是仔细阅读题目,从题目中得到因式分解的方法,难度不大.

练习册系列答案
相关题目
11. 如图,在一笔直的海岸线l上有A、B两个观测站,C离海岸线l的距离(即CD的长)为2,从A测得船C在北偏东45°的方向,从B测得船C在北偏东22.5°的方向,则AB的长( )
如图,在一笔直的海岸线l上有A、B两个观测站,C离海岸线l的距离(即CD的长)为2,从A测得船C在北偏东45°的方向,从B测得船C在北偏东22.5°的方向,则AB的长( )
 如图,在一笔直的海岸线l上有A、B两个观测站,C离海岸线l的距离(即CD的长)为2,从A测得船C在北偏东45°的方向,从B测得船C在北偏东22.5°的方向,则AB的长( )
如图,在一笔直的海岸线l上有A、B两个观测站,C离海岸线l的距离(即CD的长)为2,从A测得船C在北偏东45°的方向,从B测得船C在北偏东22.5°的方向,则AB的长( )| A. | 2km | B. | (2+$\sqrt{2}$)km | C. | (4-2$\sqrt{2}$)km | D. | (4-$\sqrt{2}$)km |
16.2x2+5x-7除以x+3的商式为ax+b,余式为c,求a+b+c=( )
| A. | -9 | B. | -5 | C. | -3 | D. | 7 |
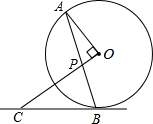 如图,AB是⊙O的弦,OP⊥OA交AB于点P,过点B的直线交OP的延长线于点C,且CP=CB.
如图,AB是⊙O的弦,OP⊥OA交AB于点P,过点B的直线交OP的延长线于点C,且CP=CB.