Question

10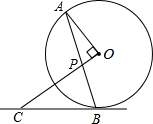．如图，AB是⊙O的弦，OP⊥OA交AB于点P，过点B的直线交OP的延长线于点C，且CP=CB．
（1）求证：BC是⊙O的切线；
（2）若⊙O的半径为$\sqrt{11}$，OP=1，求OC的长．

Answer 1

分析 （1）由垂直定义得∠A+∠APO=90°，根据等腰三角形的性质由CP=CB得∠CBP=∠CPB，根据对顶角相等得∠CPB=∠APO，因此∠APO=∠CBP，而∠A=∠OBA，得出∠OBC=∠CBP+∠OBA=∠APO+∠A=90°，然后根据切线的判定定理得到BC是⊙O的切线；
（2）设BC=x，则PC=x，在Rt△OBC中，根据勾股定理得到（ $\sqrt{11}$）²+x²=（x+1）²，然后解方程求出PC，即可得出OC的长．

解答 （1）证明：连接OB，如图所示：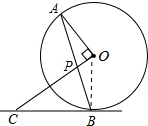
∵OP⊥OA，
∴∠AOP=90°，
∴∠A+∠APO=90°，
∵CP=CB，
∴∠CBP=∠CPB，
而∠CPB=∠APO，
∴∠APO=∠CBP，
∵OA=OB，
∴∠A=∠OBA，
∴∠OBC=∠CBP+∠OBA=∠APO+∠A=90°，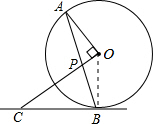
∴OB⊥BC，
∴BC是⊙O的切线；
（2）解：设BC=x，则PC=x，
在Rt△OBC中，OB=$\sqrt{11}$，OC=CP+OP=x+1，
∵OB²+BC²=OC²，
∴（$\sqrt{11}$）²+x²=（x+1）²，
解得：x=5，
即BC的长为5，
∴CP=5，
∴OC=CP+OP=5+1=6．

点评 本题考查了切线的判定定理、等腰三角形的性质、直角三角形的性质、勾股定理；熟练掌握切线的判定，由勾股定理得出方程是解决（2）的关键．