题目内容
10.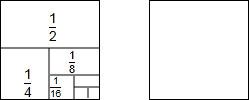 (1)请用多种方法计算:$\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{8}$+$\frac{1}{16}$+$\frac{1}{32}$+$\frac{1}{64}$+$\frac{1}{128}$.
(1)请用多种方法计算:$\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{8}$+$\frac{1}{16}$+$\frac{1}{32}$+$\frac{1}{64}$+$\frac{1}{128}$.(2)由上式计算可联想到如图,你还能联想出其他的分隔图形吗?完成提示作图,并展开联想自由作图.
(3)通过对图的分割理解,请计算:$\underset{\underbrace{\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\frac{1}{32}+\frac{1}{64}+\frac{1}{128}…}}{无穷多个}$=1.
分析 (1)①根据等比数列的求和公式计算.
②首先把每个加数分成两个分数的差的形式,然后应用加法结合律,求出算式的值是多少即可.
(2)根据算式$\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{8}$+$\frac{1}{16}$+$\frac{1}{32}$+$\frac{1}{64}$+$\frac{1}{128}$中每个加数都是和它相邻的后面的加数的2倍,画出其它的分隔图形即可.
(3)通过对图的分割理解可知:$\underset{\underbrace{\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\frac{1}{32}+\frac{1}{64}+\frac{1}{128}…}}{无穷多个}$=1,据此解答即可.
解答 解:(1)①$\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{8}$+$\frac{1}{16}$+$\frac{1}{32}$+$\frac{1}{64}$+$\frac{1}{128}$
=$\frac{\frac{1}{2}×[1{-(\frac{1}{2})}^{7}]}{1-\frac{1}{2}}$
=$\frac{\frac{1}{2}×\frac{127}{128}}{\frac{1}{2}}$
=$\frac{127}{128}$
②$\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{8}$+$\frac{1}{16}$+$\frac{1}{32}$+$\frac{1}{64}$+$\frac{1}{128}$
=1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{4}$+$\frac{1}{4}$-$\frac{1}{8}$+$\frac{1}{8}$-$\frac{1}{16}$+$\frac{1}{16}$-$\frac{1}{32}$+$\frac{1}{32}$-$\frac{1}{64}$+$\frac{1}{64}$-$\frac{1}{128}$
=1-$\frac{1}{128}$
=$\frac{127}{128}$
(2)如图1,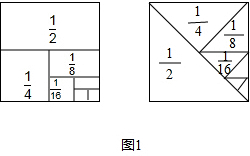 .
.
(3)$\underset{\underbrace{\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\frac{1}{32}+\frac{1}{64}+\frac{1}{128}…}}{无穷多个}$=1.
故答案为:1.
点评 (1)此题主要考查了图形的变化类问题,要熟练掌握,解答此类问题的关键是首先应找出图形哪些部分发生了变化,是按照什么规律变化的,通过分析找到各部分的变化规律后直接利用规律求解.
(2)此题还考查了数字的变化类问题,认真观察、仔细思考,善用联想是解决这类问题的方法,注意观察总结规律,并能正确的应用规律.

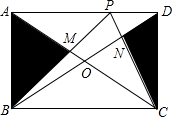 如图所示,矩形ABCD的面积为36平方厘米,四边形PMON的面积是3平方厘米,则阴影部分的面积是12平方厘米.
如图所示,矩形ABCD的面积为36平方厘米,四边形PMON的面积是3平方厘米,则阴影部分的面积是12平方厘米.