题目内容
15.若△ABC中,3∠A>5∠B,3∠C≤2∠B,则△ABC是钝角三角形.分析 三角形分锐角,直角,钝角三角形三种.判断种类只需看最大角即可.
解答 解::∵3∠A>5∠B,3∠C≤2∠B,得∠B<$\frac{3}{5}$∠A,∠C≤$\frac{2}{3}$∠B
∴∠C<$\frac{2}{5}$∠A
∴∠B+∠C<∠A
∵∠A+∠B+∠C=180°,
∴2(∠B+∠C)<180°,
∴∠B+∠C<90°,
∴-(∠B+∠C)>-90°,
∴180°-(∠B+∠C)>180°-90°=90°
即∠A>90°.
∴△ABC是钝角三角形,
故答案为:钝角.
点评 本题考查了三角形的内角和定理的应用,应用了三角形的内角和等于180°求解,是基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.2015年5月31日,我国飞人苏炳添在美国尤金举行的国际田联钻石联赛100米男子比赛中,获得好成绩,成为历史上首位突破10秒大关的黄种人.如表是苏炳添近五次大赛参赛情况:
则苏炳添这五次比赛成绩的众数和平均数分别为( )
| 比赛日期 | 2012-8-4 | 2013-5-21 | 2014-9-28 | 2015-5-20 | 2015-5-31 |
| 比赛地点 | 英国伦敦 | 中国北京 | 韩国仁川 | 中国北京 | 美国尤金 |
| 成绩(秒) | 10.19 | 10.06 | 10.10 | 10.06 | 9.99 |
| A. | 10.06秒,10.06秒 | B. | 10.10秒,10.06秒 | C. | 10.06秒,10.08秒 | D. | 10.08秒,10.06秒 |
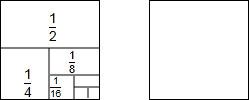 (1)请用多种方法计算:$\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{8}$+$\frac{1}{16}$+$\frac{1}{32}$+$\frac{1}{64}$+$\frac{1}{128}$.
(1)请用多种方法计算:$\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{8}$+$\frac{1}{16}$+$\frac{1}{32}$+$\frac{1}{64}$+$\frac{1}{128}$.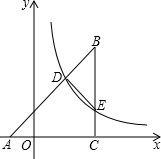 如图,等腰直角三角形ABC顶点A在x轴上,∠BCA=90°,AC=BC=2$\sqrt{2}$,反比例函数y=$\frac{3}{x}$(x>0)的图象分别与AB,BC交于点D,E.连结DE,当△BDE∽△BCA时,点E的坐标为($\frac{3}{2}\sqrt{2}$,$\sqrt{2}$).
如图,等腰直角三角形ABC顶点A在x轴上,∠BCA=90°,AC=BC=2$\sqrt{2}$,反比例函数y=$\frac{3}{x}$(x>0)的图象分别与AB,BC交于点D,E.连结DE,当△BDE∽△BCA时,点E的坐标为($\frac{3}{2}\sqrt{2}$,$\sqrt{2}$).