题目内容
4.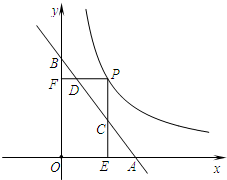 如图所示,直线y=-x+2分别与x轴、y轴交于点A、B,点P为函数y=$\frac{\sqrt{2}}{x}$ (x>0)图象上的一点,过点P分别作x轴、y轴的垂线段PE、PF,当PE、PF分别与线段AB交于点C、D时,则AD•BC的值为2$\sqrt{2}$.
如图所示,直线y=-x+2分别与x轴、y轴交于点A、B,点P为函数y=$\frac{\sqrt{2}}{x}$ (x>0)图象上的一点,过点P分别作x轴、y轴的垂线段PE、PF,当PE、PF分别与线段AB交于点C、D时,则AD•BC的值为2$\sqrt{2}$.
分析 先设P点的坐标为(a,$\frac{\sqrt{2}}{a}$),则把y=$\frac{\sqrt{2}}{a}$代入直线y=-x+2即可求出C点的纵坐标,同理求出D点坐标,再根据直线y=-x+2的解析式求出出A、B两点的坐标,再根据两点间的距离公式即可求出AD•BC的值.
解答 解:设P点的坐标为(a,$\frac{\sqrt{2}}{a}$),则C(a,2-a)、D(2-$\frac{\sqrt{2}}{a}$,$\frac{\sqrt{2}}{a}$),
∵直线y=-x+2分别与x轴、y轴交于点A、B,
∴A(2,0)、B(0,2),
∴AD•BC=$\sqrt{(2-\frac{\sqrt{2}}{a}-2)^{2}+(\frac{\sqrt{2}}{a}-0)^{2}}$•$\sqrt{(a-0)^{2}+(2-a-2)^{2}}$=$\frac{2}{a}$•$\sqrt{2}$a=2$\sqrt{2}$.
故答案为2$\sqrt{2}$.
点评 本题考查的是一次函数及反比例函数的性质,先设出P点坐标,再求出表C、D两点的坐标是解答此题的关键.

练习册系列答案
相关题目
4.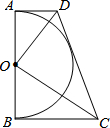 如图,在直角梯形ABCD中AD∥BC.∠ABC=90°DC与以AB为直径的半圆⊙O相切,⊙O的半径为r,在下列结论:①OD⊥OC;②AD+BC=DC; ③S△AOD+S△BOC=S△DOC; ④AD•BC=r2中正确的个数有( )
如图,在直角梯形ABCD中AD∥BC.∠ABC=90°DC与以AB为直径的半圆⊙O相切,⊙O的半径为r,在下列结论:①OD⊥OC;②AD+BC=DC; ③S△AOD+S△BOC=S△DOC; ④AD•BC=r2中正确的个数有( )
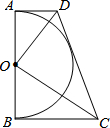 如图,在直角梯形ABCD中AD∥BC.∠ABC=90°DC与以AB为直径的半圆⊙O相切,⊙O的半径为r,在下列结论:①OD⊥OC;②AD+BC=DC; ③S△AOD+S△BOC=S△DOC; ④AD•BC=r2中正确的个数有( )
如图,在直角梯形ABCD中AD∥BC.∠ABC=90°DC与以AB为直径的半圆⊙O相切,⊙O的半径为r,在下列结论:①OD⊥OC;②AD+BC=DC; ③S△AOD+S△BOC=S△DOC; ④AD•BC=r2中正确的个数有( )| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
13.同一副三角板(两块)画角,不可能画出的角的度数是( )
| A. | 135° | B. | 75° | C. | 55° | D. | 15° |
14.在△ABC中,∠C=90°,AB=12,BC=5,则AC的长为( )
| A. | 12 | B. | 13 | C. | $\sqrt{119}$ | D. | 15 |

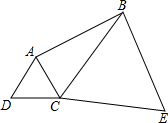 如图,△ADC和△BCE都是等边三角形,已知BD2=AB2+BC2,那么∠ABC=30°.
如图,△ADC和△BCE都是等边三角形,已知BD2=AB2+BC2,那么∠ABC=30°.