题目内容
20.四边形ABCD中,AC⊥BD,AB、BC、CD、AD的中点分别是E、F、G、H,则四边形EFGH一定是( )| A. | 矩形 | B. | 菱形 | C. | 正方形 | D. | 梯形 |
分析 有一个角是直角的平行四边形是矩形.利用中位线定理可得出四边形EFGH矩形.
解答  解:∵点E、F分别为四边形ABCD的边AD、AB的中点,
解:∵点E、F分别为四边形ABCD的边AD、AB的中点,
∴EF∥BD,且EF=$\frac{1}{2}$BD.
同理求得EH∥AC∥GF,且EH=GF=$\frac{1}{2}$AC,
又∵AC⊥BD,
∴EF∥GH,FG∥HE且EF⊥FG.
四边形EFGH是矩形.
故选:A.
点评 本题考查的是中点四边形.解题时,利用了矩形的判定以及矩形的定理,矩形的判定定理有:
(1)有一个角是直角的平行四边形是矩形;
(2)有三个角是直角的四边形是矩形;
(3)对角线互相平分且相等的四边形是矩形.

练习册系列答案
 综合自测系列答案
综合自测系列答案
相关题目
5.已知数据x1、x2、x3的平均数为m,数据y1、y2的平均数为n,那么数据x1、x2、x3、y1、y2的平均数为( )
| A. | m+n | B. | $\frac{m+n}{2}$ | C. | $\frac{m+n}{5}$ | D. | $\frac{3m+2n}{5}$ |




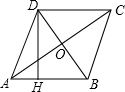 如图,四边形ABCD是菱形,对角线AC和BD相交于点O,AC=8cm,BD=6cm,DH⊥AB于H.
如图,四边形ABCD是菱形,对角线AC和BD相交于点O,AC=8cm,BD=6cm,DH⊥AB于H.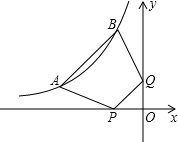 如图,点A(a,2)、B(-2,b)都在双曲线y=$\frac{k}{x}(x<0)$上,点P、Q分别是x轴、y轴上的动点,当四边形PABQ的周长取最小值时,PQ所在直线的解析式是y=x+$\frac{3}{2}$,则k=-7.
如图,点A(a,2)、B(-2,b)都在双曲线y=$\frac{k}{x}(x<0)$上,点P、Q分别是x轴、y轴上的动点,当四边形PABQ的周长取最小值时,PQ所在直线的解析式是y=x+$\frac{3}{2}$,则k=-7.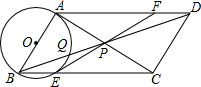 如图,在?ABCD中,∠BAC=90°,对角线AC,BD相交于点P,以AB为直径的⊙O分别交BC,BD于点E,Q,连接EP并延长交AD于点F.
如图,在?ABCD中,∠BAC=90°,对角线AC,BD相交于点P,以AB为直径的⊙O分别交BC,BD于点E,Q,连接EP并延长交AD于点F.