题目内容
12.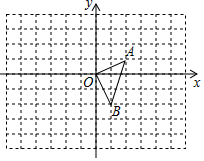 如图,在平面直角坐标系中,△OAB的顶点坐标分别为(0,0),A(2,1),B(1,-2).
如图,在平面直角坐标系中,△OAB的顶点坐标分别为(0,0),A(2,1),B(1,-2).(1)以原点O为位似中心,在y轴的右侧画出△OAB的一个位似△OA1B1,使它与△OAB的位似比为2:1,并分别写出点A、B的对应点A1、B1的坐标;
(2)画出将△OAB向左平移2个单位,再向上平移1个单位后得△O2A2B2,并写出点A、B的对应点A2、B2的坐标;
(3)判断△OA1B1和△O2A2B2是位似图形吗?若是,请在图中标出位似中心 M,并写出点M的坐标.
分析 (1)分别延长OA、OB,使OA1=2OA,OB1=2OB,则△OA1B1满足条件,然后写出点A1、B1的坐标;
(2)利用点平移的坐标规律写出O2、A2、B2的坐标,然后描点即可;
(3)延长A1A2、B1B2、OO2,它们相交于一点,则可判定△OA1B1和△O2A2B2是位似图形,然后写交点坐标.
解答 解:(1)如图,△OA1B1为所作,点A1、B1的坐标分别为(4,2),(2,-4);
(2)如图,△O2A2B2为所作,点A2、B2的坐标分别为(0,2),(-1,-1);
(3)△OA1B1和△O2A2B2是位似图形,如图,点M为所,位似中心 M的坐标为(4,2).
点评 本题考查了作图-位似变换:先确定位似中心;再分别连接并延长位似中心和能代表原图的关键点;接着根据位似比,确定能代表所作的位似图形的关键点;然后顺次连接上述各点,得到放大或缩小的图形.

练习册系列答案
相关题目

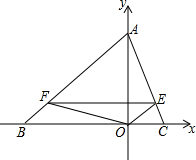 如图,等腰△ABC中,BA=BC,AO=3CO=6.动点F在BA上以每分钟5个单位长度的速度从B点出发向A点移动,过F作FE∥BC交AC边于E点,连结FO、EO.
如图,等腰△ABC中,BA=BC,AO=3CO=6.动点F在BA上以每分钟5个单位长度的速度从B点出发向A点移动,过F作FE∥BC交AC边于E点,连结FO、EO. 如图,线段AB=8,M是线段AB的中点,N是线段AC的中点,C为线段AB上一点,且AC=3.2,求M,N两点间的距离.
如图,线段AB=8,M是线段AB的中点,N是线段AC的中点,C为线段AB上一点,且AC=3.2,求M,N两点间的距离.