Question

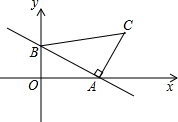
已知抛物线y=ax²+x+c（a≠0）经过A（-1，0），B（2，0）两点，与y轴相交于点C，该抛物线的顶点为点M，对称轴与BC相交于点N，与x轴交于点D．
（1）求该抛物线的解析式及点M的坐标；
（2）连接ON，AC，证明：∠NOB=∠ACB；
（3）点E是该抛物线上一动点，且位于第一象限，当点E到直线BC的距离为

2

2

时，求点E的坐标；
（4）在满足（3）的条件下，连接EN，并延长EN交y轴于点F，E、F两点关于直线BC对称吗？请说明理由．

Answer 1

考点：二次函数综合题,勾股定理的应用

专题：

分析：（1）利用待定系数法即可求得解析式，把解析式转化成顶点式即可求得顶点坐标．
（2）根据有两组对应边对应成比例且夹角相等即可求得△ABC∽△NBO，由三角形相似的性质即可求得．
（3）作EQ⊥BC于Q，根据抛物线的解析式先设出E点的坐标，然后根据两直线垂直的性质求得Q点的坐标，根据勾股定理即可求得．
（4）先求得直线EF的解析式，即可求得BC⊥EF，根据勾股定理求得EN=FN，即可判定E、F两点关于直线BC对称．

解答：解：（1）∵抛物线y=ax²+x+c（a≠0）经过A（-1，0），B（2，0）两点，
∴

a-1+c=0 4a+2+c=0

，
 解得

a=-1 c=2

．
∴抛物线为y=-x²+x+2；
∴抛物线为y=-x²+x+2=-（x-

1

2

）²+

9

4

，
∴顶点M（

1

2

，

9

4

）．

（2）如图1，∵A（-1，0），B（2，0），C（0，2），
∴直线BC为：y=-x+2，
当x=

1

2

时，y=

3

2

，
∴N（

1

2

，

3

2

），
∴AB=3，BC=2

2

，OB=2，BN=

(2- 1 2 )2+( 3 2 )2

=

3

2

2

，
∴

AB

BC

=

3

2 2

=

3 2

4

，

BN

OB

=

3 2 2

2

=

3 2

4

，
∵∠ABC=∠NBO，
∴△ABC∽△NBO，
∴∠NOB=∠ACB；

（3）如图2，作EQ⊥BC于Q，
∵直线BC为y=-x+2，
∴设E（m，-m²+m+2），
直线EQ的解析式为y=x+b，
则直线EQ为y=x+（-m²+2），
解

y=-x+2 y=x+(-m2+2)

得

x= 1 2 m y=- 1 2 m2+2

，
∴Q（

1

2

m²，-

1

2

m²+2），
∵EQ=

2

2

，
∴（m-

1

2

m²）²+（-

1

2

m²+2+m²-m-2）²=（

2

2

）²，
解得m=1，
∴-m²+m+2=2，
∴E（1，2），

（4）如图2，连接EN，并延长EN交y轴于点F，
∵E（1，2），N（

1

2

，

3

2

），
设直线EN的解析式为y=ax+b，
∴

a+b=2 1 2 a+b= 3 2

，解得

a=1 b=1

，
∴直线EF为y=x+1，
∴F（0，1），
∵直线BC和直线EF斜率互为负倒数，
∴EF⊥BC，
∴EN=

(1- 1 2 )2+(2- 3 2 )2

=

2

2

，FN=

( 1 2 )2+( 3 2 -1)2

=

2

2

，
∴EN=FN，
∴E、F两点关于直线BC对称．

点评：本题考查了待定系数法求解析式，抛物线的顶点的求法，直线的交点问题，勾股定理的应用等．