Question

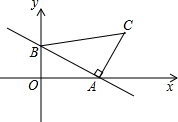如图，一次函数y=-

2

3

x+2的图象分别与x轴、y轴交于点A、B，以线段AB为边在第一象限内作等腰Rt△ABC，∠BAC=90°．
（1）求点C的坐标；
（2）在x轴上求一点P，使它到B、C两点的距离之和最小．

Answer 1

考点：轴对称-最短路线问题,一次函数的性质,等腰直角三角形

专题：

分析：（1）先根据一次函数的解析式求出A、B两点的坐标，再作CD⊥x轴于点D，由全等三角形的判定定理可得出△ABO≌△CAD，由全等三角形的性质可知OA=CD，故可得出C点坐标；
（2）求得B关于x轴的对称点B′，利用待定系数法求得B′C的解析式，然后求得与x轴的交点即可．

解答：解：（1）在一次函数y=-

2

3

x+2中，
令x=0得：y=2；
令y=0，解得x=3，
则B的坐标是（0，2），A的坐标是（3，0）．   
如图，作CD⊥x轴于点D．
∵∠BAC=90°，
∴∠OAB+∠CAD=90°，
又∵∠CAD+∠ACD=90°，
∴∠ACD=∠BAO．
在△ABO与△CAD中，

∠BAO=∠ACD ∠BOA=∠ADC=90° AB=CA

，
∴△ABO≌△CAD（AAS），
∴OB=AD=2，OA=CD=3，OD=OA+AD=5．
则C的坐标是（5，3）． 
                   
（2）B关于x轴的对称点的坐标是B′（0，-2），
设直线B′C的解析式是y=kx+b，
根据题意得：

5k+b=3 b=-2

，
解得：

k=1 b=-2

，
∴直线B′C的解析式是y=x-2．
令y=0，解得：x=2，
则P的坐标是：（2，0）．

点评：本题考查的是一次函数综合题，涉及到用待定系数法求一次函数的解析式、全等三角形的判定与性质，根据题意作出辅助线，构造出全等三角形是解答此题的关键．