题目内容
1.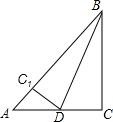 如图,已知Rt△ABC中,直角边AC=6,BC=8,∠C=90°,将△ABC沿BD所在直线折叠使BC落在AB上,点C落在C1处,求折叠后重合部分△BDC1的面积.
如图,已知Rt△ABC中,直角边AC=6,BC=8,∠C=90°,将△ABC沿BD所在直线折叠使BC落在AB上,点C落在C1处,求折叠后重合部分△BDC1的面积.
分析 利用勾股定理列式求出AB,根据折叠的性质可得BC1=BC,CD=C1D,∠BC1D=∠C=90°,然后求出AC1,设C1D=CD=x,表示出AD,再利用勾股定理列出方程求出x,然后利用三角形的面积公式列式计算即可得解.
解答 解:∵BC=8,AC=6,
∴AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=10,
∵△BCD沿BD折叠,C落在AB边上的C1处,
∴BC1=BC=8,CD=C1D,∠BC1D=∠C=90°,S△BDC1=S△BCD,
∴AC1=AB-BC1=10-8=2,
设C1D=CD=x,则AD=6-x,
在Rt△AC1D中,AD2=AC12+C1D2,
即(6-x)2=22+x2,
解得x=$\frac{8}{3}$,
∴S△BDC1=S△BCD=$\frac{1}{2}$×8×$\frac{8}{3}$=$\frac{32}{3}$.
点评 本题考查了翻折变换的性质,勾股定理,主要利用了翻折前后的两个图形对应边相等,对应角相等,利用勾股定理列出方程求出CD的长度是解题的关键.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
11.下列各题计算正确的是( )
| A. | (ab-1)(-4ab2)=-4a2b3-4ab2 | B. | (3x2+xy-y2)•3x2=9x4+3x3y-y2 | ||
| C. | (-3a)(a2-2a+1)=-3a3+6a2 | D. | (-2x)(3x2-4x-2)=-6x3+8x2+4x |
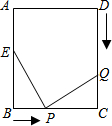 如图,已知长方形ABCD的边长AB=16cm,BC=12cm,点E在边AB上,AE=6cm,如果点P从点B出发在线段BC上以2cm/s的速度向点C向运动,同时,点Q在线段CD上由点D向C点运动.则当△BPE与△CQP全等时,P运动时间t为1或3s.
如图,已知长方形ABCD的边长AB=16cm,BC=12cm,点E在边AB上,AE=6cm,如果点P从点B出发在线段BC上以2cm/s的速度向点C向运动,同时,点Q在线段CD上由点D向C点运动.则当△BPE与△CQP全等时,P运动时间t为1或3s.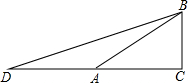 如图所示,在△ABC中,∠C=90°,D是CA延长线上一点,∠BDC=15°,AD=AB=4,则BC=2.
如图所示,在△ABC中,∠C=90°,D是CA延长线上一点,∠BDC=15°,AD=AB=4,则BC=2.