题目内容
9.已知8+2$\sqrt{3}$的小数部分是m,8-2$\sqrt{3}$的小数部分是n,求m-n的值.分析 先估算出2$\sqrt{3}$=$\sqrt{12}$的取值范围,进而可得出m、n的值,代入m-n进行计算即可.
解答 解:2$\sqrt{3}$=$\sqrt{12}$,
∵9<12<16,
∴3<$\sqrt{12}$<4,-4<-$\sqrt{12}$<-3,
∴11<8+2$\sqrt{3}$<12,4<8-2$\sqrt{3}$<5,
∴8+2$\sqrt{3}$的小数部分m=8+2$\sqrt{3}$-11=2$\sqrt{3}$-3,8-2$\sqrt{3}$的小数部分是n=8-2$\sqrt{3}$-4=4-2$\sqrt{3}$,
∴m-n=2$\sqrt{3}$-3-(4-2$\sqrt{3}$)=4$\sqrt{3}$-7.
点评 此题考查无理数的估算,注意确定无理数的整数部分即可解决问题.

练习册系列答案
相关题目
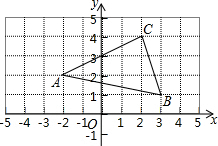 如图,边长为1的正方形网格中有格点△ABC和格点O,若把△ABC绕着点O逆时针旋转180°
如图,边长为1的正方形网格中有格点△ABC和格点O,若把△ABC绕着点O逆时针旋转180°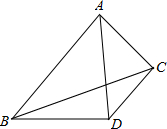 如图,△ABC中,AB=2AC,AD平分∠BAC,且AD=BD.求证:CD⊥AC.
如图,△ABC中,AB=2AC,AD平分∠BAC,且AD=BD.求证:CD⊥AC.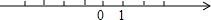 已知在纸面上有一数轴(如图),折叠纸面.
已知在纸面上有一数轴(如图),折叠纸面.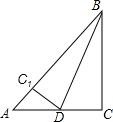 如图,已知Rt△ABC中,直角边AC=6,BC=8,∠C=90°,将△ABC沿BD所在直线折叠使BC落在AB上,点C落在C1处,求折叠后重合部分△BDC1的面积.
如图,已知Rt△ABC中,直角边AC=6,BC=8,∠C=90°,将△ABC沿BD所在直线折叠使BC落在AB上,点C落在C1处,求折叠后重合部分△BDC1的面积.