题目内容
5.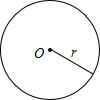 已知⊙O的半径为r.
已知⊙O的半径为r.(1)此圆的周长=2πr,面积S=πr2.
(2)1°的圆心角所对的弧长叫做1°的弧长,那么,上述圆的1°的弧长=$\frac{πr}{180}$,n°的圆心角所对的弧长=$\frac{nπr}{180}$.
分析 (1)由圆的周长公式和面积公式即可得出结果;
(2)由1°的弧长的定义和弧长的推导即可得出结果.
解答 解:(1)∵⊙O的半径为r,
∴圆的周长=2πr,面积S=πr2;
故答案为:2πr,πr2.
(2)1°的圆心角所对的弧长叫做1°的弧长,
那么,上述圆的1°的弧长=$\frac{2πr}{360}$=$\frac{πr}{180}$,n°的圆心角所对的弧长=$\frac{nπr}{180}$;
故答案为:1°,$\frac{πr}{180}$,$\frac{nπr}{180}$.
点评 本题考查了圆的周长、面积公式以及弧长公式;熟练掌握圆的周长和面积以及弧长公式,正确熟记这些重要公式是关键.

练习册系列答案
相关题目
16.已知a+b=5,ab=4,则ab2+a2b-a-b的值是( )
| A. | -15 | B. | 15 | C. | 6 | D. | -6 |
15. 如图,射线BA、CA交于点A.连接BC,已知∠B=∠C=40°,那么∠α=( )度.
如图,射线BA、CA交于点A.连接BC,已知∠B=∠C=40°,那么∠α=( )度.
 如图,射线BA、CA交于点A.连接BC,已知∠B=∠C=40°,那么∠α=( )度.
如图,射线BA、CA交于点A.连接BC,已知∠B=∠C=40°,那么∠α=( )度.| A. | 60 | B. | 70 | C. | 80 | D. | 90 |
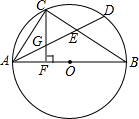 AB是⊙O的直径,D是$\widehat{AB}$上的一点,C是$\widehat{AD}$的中点,AD,BC相交于E,CF⊥AB,F为垂足,CF交AD于G,求证:①CG=EG=AG;②AD=2CF.
AB是⊙O的直径,D是$\widehat{AB}$上的一点,C是$\widehat{AD}$的中点,AD,BC相交于E,CF⊥AB,F为垂足,CF交AD于G,求证:①CG=EG=AG;②AD=2CF.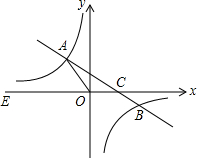 如图,在平面直角坐标系xOy中,一次函数的图象y=kx+b(k≠0)与反比例函数y=$\frac{m}{x}$(m≠0)的图象交于二、四象限内的A、B两点,与x轴交于C点,线段OA=5,OC=3,E为x轴上一点,且tan∠AOE=$\frac{4}{3}$.
如图,在平面直角坐标系xOy中,一次函数的图象y=kx+b(k≠0)与反比例函数y=$\frac{m}{x}$(m≠0)的图象交于二、四象限内的A、B两点,与x轴交于C点,线段OA=5,OC=3,E为x轴上一点,且tan∠AOE=$\frac{4}{3}$.