题目内容
8.已知关于x的方程x2+x+2a-1=0的一个根是0,则a=$\frac{1}{2}$.分析 方程的解就是能使方程左右两边相等的未知数的值,把x=0代入方程,即可得到一个关于a的方程,即可求得a的值.
解答 解:根据题意得:0+0+2a-1=0
解得a=$\frac{1}{2}$.
故答案为:$\frac{1}{2}$.
点评 本题考查了一元二次方程的解.一元二次方程的根一定满足该方程的解析式.

练习册系列答案
相关题目
19.某体校要从四名射击选手中选拔一名参加省体育运动会,选拔赛中每名选手连续射靶10次,他们各自的平均成绩$\overline{x}$及其方差S2如表所示:
如果要选出一名成绩高且发挥稳定的选手参赛,则应选择的选手是( )
| 甲 | 乙 | 丙 | 丁 | |
| $\overline{x}$(环) | 8.4 | 8.6 | 8.6 | 7.6 |
| S2 | 0.74 | 0.56 | 0.94 | 1.92 |
| A. | 甲 | B. | 乙 | C. | 丙 | D. | 丁 |
3.计算:5x-3x=( )
| A. | 2x | B. | 2x2 | C. | -2x | D. | -2 |
13.已知x1,x2是关于x的方程x2+ax-2b=0的两实数根,且x1+x2=-2,x1•x2=1,则ba的值是( )
| A. | $\frac{1}{4}$ | B. | -$\frac{1}{4}$ | C. | 4 | D. | -1 |
5.下列各式中,计算正确的是( )
| A. | x(2x-1)=2x2-1 | B. | $\frac{x+3}{{x}^{2}-9}$=$\frac{1}{x-3}$ | C. | (a+2)2=a2+4 | D. | (x+2)(x-3)=x2+x-6 |
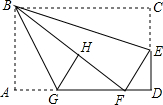 如图,在矩形纸片ABCD中,AB=6,BC=10,点E在CD上,将△BCE沿BE折叠,点C恰落在边AD上的点F处;点G在AF上,将△ABG沿BG折叠,点A恰落在线段BF上的点H处,有下列结论:
如图,在矩形纸片ABCD中,AB=6,BC=10,点E在CD上,将△BCE沿BE折叠,点C恰落在边AD上的点F处;点G在AF上,将△ABG沿BG折叠,点A恰落在线段BF上的点H处,有下列结论: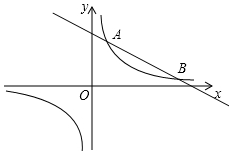 如图,反比例函数y=$\frac{m}{x}$的图象与一次函数y=kx+b的图象交于A,B两点,点A的坐标为(2,6),点B的坐标为(n,1).
如图,反比例函数y=$\frac{m}{x}$的图象与一次函数y=kx+b的图象交于A,B两点,点A的坐标为(2,6),点B的坐标为(n,1).