题目内容
在△ABC中，∠A=60°，∠B比∠C大10°，求∠C的度数．
考点：三角形内角和定理
专题：
分析：设∠C=α，则∠B=α+10°；由内角和定理列出关于α的方程，即可解决问题．
解答：解：设∠C=α，则∠B=α+10°；
由内角和定理得：
α+α+10°+60°=180°，
∴α=55°，
即∠C=55°．
由内角和定理得：
α+α+10°+60°=180°，
∴α=55°，
即∠C=55°．
点评：该题主要考查了三角形的内角和定理及其应用问题；解题的关键是灵活运用有关定理来分析、判断、推理或解答．
练习册系列答案
相关题目
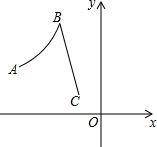如图，已知A点坐标为（-6，3），C点坐标为（-2，1），曲线段AB是反比例函数图象的一部分，线段BC是一次函数图象的一部分，若B点到x轴的距离等于到y轴距离的2倍．函数y=2-
的最值是（ ）
| -x2+4x |
| A、y最小值=-2，y最大值=2 | ||||
| B、y最小值=1，y最大值=2 | ||||
| C、y最小值=0，y最大值=2 | ||||
D、y最小值=-
|