题目内容
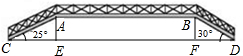 如图是新城市建设中设计的一条人行过街天桥平面设计图,已知桥面AB与地面DC平行,立柱AE⊥CD于点E,立柱BF⊥CD于点F,CD=87.1m,CE=15m,∠ACE=25°,∠BDF=30°
如图是新城市建设中设计的一条人行过街天桥平面设计图,已知桥面AB与地面DC平行,立柱AE⊥CD于点E,立柱BF⊥CD于点F,CD=87.1m,CE=15m,∠ACE=25°,∠BDF=30°(1)求平面AB与地面CD之间的距离(精确到0.1);
(2)求桥面AB的长(精确到0.1m);
(参与数据:sin25°=0.42,cos25°=0.91,tan 25°=0.466,
| 2 |
| 3 |
考点:解直角三角形的应用
专题:
分析:(1)在Rt△ACE中,根据三角函数可求AE的长;
(2)首先判定四边形ABFE为矩形,在Rt△BFD中,根据三角函数得到DF,再根据AB=EF=CD-CE-DF即可求解.
(2)首先判定四边形ABFE为矩形,在Rt△BFD中,根据三角函数得到DF,再根据AB=EF=CD-CE-DF即可求解.
解答:解:(1)在Rt△ACE中,∠ACE=25°,CE=15m,
AE=CE•tan25°=15×0.466≈7.0(m).
答:平面AB与地面CD之间的距离约为7.0m;
(2)∵AE⊥CD,BF⊥CD,
∴AE∥BF,∠AEF=90°,
∵AB∥EF,
∴四边形ABFE为矩形,
∴AB=EF,AE=BF=7.0,
在Rt△BFD中,∠BDF=30°,BF=7.0m,
∴DF=
=
BF=1.73×7.0≈12.1m,
∴AB=EF=CD-CE-DF=87.1-15-12.1=60m.
答:桥面AB的长约为60m.
AE=CE•tan25°=15×0.466≈7.0(m).
答:平面AB与地面CD之间的距离约为7.0m;
(2)∵AE⊥CD,BF⊥CD,
∴AE∥BF,∠AEF=90°,
∵AB∥EF,
∴四边形ABFE为矩形,
∴AB=EF,AE=BF=7.0,
在Rt△BFD中,∠BDF=30°,BF=7.0m,
∴DF=
| BF |
| tan30° |
| 3 |
∴AB=EF=CD-CE-DF=87.1-15-12.1=60m.
答:桥面AB的长约为60m.
点评:此题考查的是解直角三角形的应用,关键是熟练掌握三角函数的知识,用数学知识解决实际问题.

练习册系列答案
 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案
相关题目
用10米长的铝材制成一个矩形窗框,使它的面积为6平方米.若设它的一条边长为x米,则根据题意可列出关于x的方程为( )
| A、x(5+x)=6 |
| B、x(5-x)=6 |
| C、x(10-x)=6 |
| D、x(10-2x)=6 |
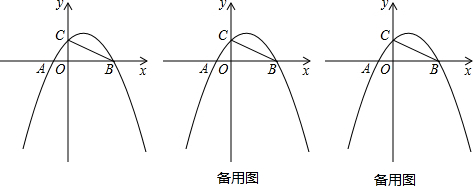
 如图,在△ABO中,OA=OB,C是边AB的中点,以O为圆心的圆过点C.
如图,在△ABO中,OA=OB,C是边AB的中点,以O为圆心的圆过点C.